Risk is the ally of the underdog

When talking about sports strategy, there are often ideas that seem counterintuitive and obvious at the same time.

This fact has become painfully clear to me during the last year and a half or so, ever since I first advanced the idea of Braess’s Paradox in basketball.  The idea (which eventually became an academic paper and a presentation at last year’s Sloan Sports conference; download the PowerPoint file here) generally prompted one of two responses: “Wow, that’s really cool” or “…why did you need a bunch of confusing diagrams and equations to say something I already knew?”.

Both responses seem perfectly reasonable to me.  As I see it, the reason for this dichotomy is that the main idea behind the “price of anarchy in basketball” can be stated in two ways:

1) “A team needs to maintain diversity of its offensive options in order to stay effective.”

OR

2) “In order to play its best possible game, a team often has to intentionally run a play that is less likely to succeed than other plays.”

While the second statement seems surprising and counterintuitive; the first seems obvious.  Both of these statements, though, are equivalent to saying “running the best possible play each time down the court is not the same as playing the best possible game.”

In general, this is a fairly common predicament: an idea can be stated in two equivalent ways, one of which sounds wrong while the other seems correct.  It is my opinion that whenever such situations arise you need a quantitative description that can be carried through to a single logical conclusion.  In this way, the logical rigor of mathematics can serve as your King Solomon, adjudicating between right and wrong.

In this post I want to discuss another sports idea that seems both obvious and counterintuitive.  The obvious phrasing goes like this:

An underdog needs to accept risk in order to give itself a real chance of winning.  A heavily-favored team, on the other hand, should try to minimize risk.

This statement has a much more counterintuitive partner, though.  Namely:

A team’s best strategy for success involves intentionally lowering its expected offensive efficiency.

In other words, sometimes an underdog needs to adopt a strategy that will lead, on average, to a worse loss.

In the remainder of this post I’ll discuss why this idea is correct and how it can be made quantitative.  Then, as an example, I’ll apply it to the following simple question: how often should a basketball team shoot the three?

Is risk your enemy or your ally?

The major point of this post is to assert and then explore the following statement: There is a significant difference between optimizing the efficiency of your offense and optimizing your chance of winning.

As an illustration of why this is true, consider the following simple example.  Imagine that you are the coach of a basketball team that trails by three points with only one shot left.  Should you tell the team to go for a two- or a three-pointer?

The answer to this question, of course, is obvious: you shoot the three.  But to understand the implications of this answer, consider how it sounds in statistical language.  Your basic choice is between a high-probability 2-point shot (which the defense will likely allow without a fight) and a low-probability 3-point shot (which they’ll probably defend carefully).  Say that you estimate the chance of making a 2-pointer at 80%, while the chance of making a 3-pointer is only 20%.  This means that, on average, calling for the two-point shot will yield points while calling for the three-point shot will give only .  So by calling for the three-point shot, you are instructing your team to make a play that is almost three times worse in terms of average number of points scored.

Think of it this way: if your team were coached by a robot that had been programmed to optimize the team’s expected number of points scored, then the robot coach would immediately order your team to go for two.  How would you explain to the robot (or its programmers) the flaw in its design?

I might say it this way: when winning is unlikely, you need to be willing to sacrifice from the average outcome in order to improve the best possible outcome.  Or, as a more general principle, an underdog must be willing to accept greater-than-average risk.

Now let me try to translate that statement into mathematical language: A team whose expected scoring output is lower than that of its opponent (an underdog) should pursue strategies with a higher variance (more “risk”), even if these result in a lower mean.

Got that?

Let me try to make the point graphically.  When your team decides on a strategy for the remainder of the game, its final number of points scored can be described by some distribution (a “probability density function”).  This distribution has some average (the mean) and some width (the standard deviation).  Similarly, your opponent has some distribution describing its own final score.  If your opponent is generally better than you, then their distribution will have a larger mean than yours.

For you to win the game requires two unlikely events to happen simultaneously: you have to happen to score near the top of the distribution, and your opponent has to score near the bottom of their distribution.  As such, the probability that you will win is represented graphically by the overlap between your distribution and that of your opponent.  More overlap means a better chance for you to pull off the upset.

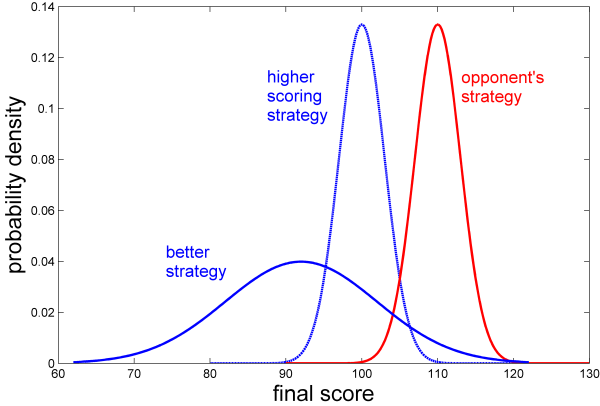The figure above shows this principle schematically.  The two blue curves represent two hypothetical possible strategies that your team can employ.  One of them results in an average final score of 100 points while the other results in an average final score of 92 points.  In this case, though, the 92-point strategy is the better one because it is accompanied by a much larger variance, so that the overlap with your opponent’s distribution is greater.

You could also say it this way: if you have an opponent who is going to score about points, a strategy that yields points is much better than a strategy that yields .

On the other hand, if it’s worthwhile for the underdog to lower their mean in order to increase their variance, then it must also be worthwhile for the favored opponent to lower their mean in order to lower its variance.  Like this:

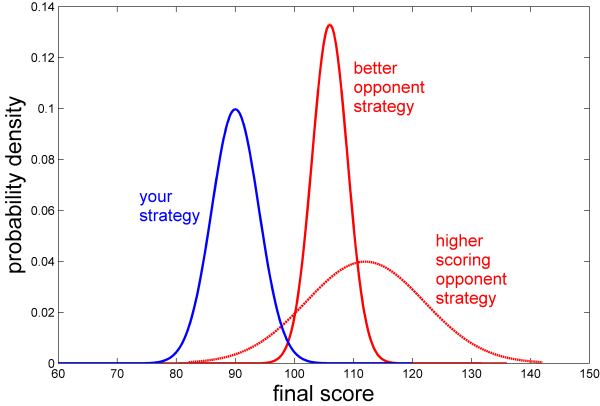In other words, if you’re the favorite to win the game, it can be worthwhile to play conservatively.  Such conservative strategies lower your average score, but they also reduce the likelihood of very low scores that would produce an upset.

So now that the tradeoff between large average score and large/small variance in score is apparent, we have an optimization problem.  How much should a team be willing to sacrifice from its average score (or average offensive efficiency) in order to increase/reduce its variance?  How much risk is the right amount?

In this post I want to show that these questions can be answered quantitatively.  As a simple example I’ll use the most straightforward risk/reward question in basketball: how often should my team shoot the 3?

Live by the three, die by the three?

In basketball, taking a three-point shot is an inherently risky play: it’ll give you more points, but you are more likely to miss.  Imagine, for example, the following scenario.  You are in the gym, shooting around, when a friend bets you $100 that you can’t score 100 points on 100 shots.  You are given the option of shooting either 2’s (from the free throw line) or shooting 3’s.    Which would you choose?

The answer, of course, depends on your shooting percentages from each spot.  Consider, for example, the following hypothetical cases:

A) You shoot 45% from the free throw line and 30% from the three-point line.

B) You shoot 54% from the free throw line and 36% from the three-point line.

Which option would you pick in each case: 2’s or 3’s?

The numbers in cases A and B are cleverly chosen so that your average number of points scored is the same no matter which option you choose.  But the risk associated with the two strategies is different.  In scenario A, for example, there is a 95% chance that your score will fall between 72 and 110 if you shoot 2’s.  If you choose to shoot 3’s, however, that same window of probability is between 63 and 120.  So your risk (lowest reasonably-likely score) is higher, but your reward (highest reasonably-likely score) is also higher.  Which should you choose?

The answer is this: if you are an underdog (scenario A, where your average score is 90 points), go for the three; risk is your ally.  If you are favored to win (scenario B, where your average score is 108 points), go for the two; risk is your enemy.

Now let’s move beyond this contrived example to a slightly less-contrived example: a hypothetical NBA team (let’s call them the Timberwolves) is considering how often they should shoot the three against a highly favored opponent (let’s call them the Lakers).  The Timberwolves can score 50% of the time if they go for the two and 30% of the time if they go for the three.  How many three-pointers should they shoot?

The Lakers, for their part, are a well-coached team who realize that they should play conservatively.  So let’s say (for the sake of argument) that they take only low-risk 2-point shots, which they make 55% of the time.  In this case, the distribution of their final score is well-known: it is given by the binomial distribution.  [*See the important footnote at the end of the post.]

In deciding how often to go for three, the Timberwolves face the following tradeoff: shooting three’s lowers their average score, but it increases the variance of their score.  What is the optimal amount?

The distribution of final scores for the Timberwolves is also given by the binomial distribution (more correctly, a combination of two binomial distributions: one for 2’s and one for 3’s).  Since both distributions are known, it is possible to calculate the probability that the Timberwolves will win the game as a function of the number of 3’s they take.  From there we can calculate the “optimal strategy” for the T-Wolves.

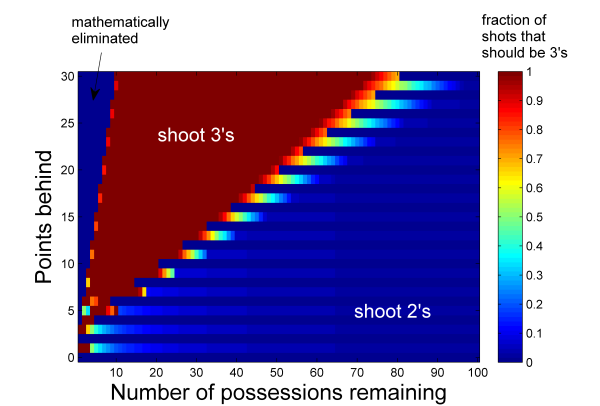
The result, shown below, depends on two crucial factors: how many possessions are left in the game, and how large a deficit the Timberwolves are facing.  When the score is close or there are many possessions left, the Timberwolves should shoot mostly 2’s, thereby optimizing their average output.  On the other hand, when the Timberwolves are facing a large deficit with only a relatively short time left, they should shoot mostly 3’s in a (somewhat) desperate attempt to catch up.

This result is pretty interesting: there are clearly-separated phases of three-point shooting and two-point shooting.  But the result is also pretty unrealistic.  For example, it says that a team down by 20 points with 30 possessions left (about a quarter and a half) should take a 3-pointer with every single shot.  In real life, such an approach is pretty unlikely to succeed.  What the model above fails to take into account, of course, is that if you start relying heavily on a particular play then the defense will start guarding that play more carefully and its effectiveness will drop.  This was the essential observation behind the “price of anarchy in basketball” analysis (and, of course, is not originally mine).

So let me present another, very slightly less contrived scenario, this time involving G&L staple Ray Allen.  Suppose your team is comprised of four decent two-point shooters and one stellar three-point shooter named Ray Allen.  The two-point shooters can score 50% of the time.  Ray Allen can score 50% of the time when used very rarely, but the more often he is called upon to shoot the three, the more his percentage will decline due to increased pressure from the defense.  Let’s say that Ray Allen’s shooting percentage is related to the fraction of the team’s shots he takes by

.

The strategy that optimizes the team’s average scoring output is for Ray Allen to shoot a fraction of the team’s shots (almost the same as everyone else), which results in the team scoring about 105 points per 100 possessions.  (Details on how to figure this out are here, or in the academic paper I linked to above).

Now let’s say that your team (with Ray Allen) is the underdog against an opponent that scores 110 points per 100 possessions (again, let’s have them be the Lakers).  In this scenario your team should carefully weigh how to use Ray Allen.  If you have him shoot about 20% of the time, you will optimize the average scoring output of your team.  If you push him to shoot more, your average scoring will suffer but the variance of your score will increase.  What is your optimal strategy?

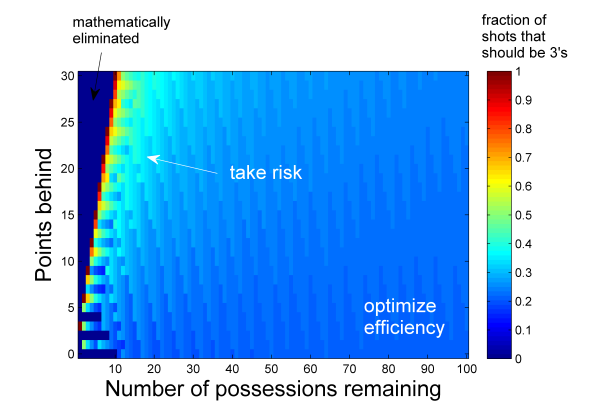
Below is the result of the calculation: the team’s optimal strategy as a function of possessions remaining and deficit.  I should admit that some of the points in the bottom left-hand corner are questionable (if your team has one shot remaining and Ray Allen takes it, is it fair to set so that Ray Allen’s shooting percentage is 10%?).  This is an inherent weakness of using deterministic “skill curve” relations like my above.

The general message, though, is pretty clear.  When there is a lot of time remaining and the lead is not too big, your team should be looking to optimize its average efficiency: have Ray Allen shoot about 20% of the time.  When you are facing a big deficit, however, it’s worth being “risky”.  In these situations, having Ray Allen shoot more than 20% of the time lowers your average score, but it increases your chance of winning.

Toward quantifying risk and reward

In the end, these are only very simplified examples of what it means to take risk in a sporting contest.  There are lots of other ways, and these have become particularly popular points of discussion during the last year or two (here, for example).  But I really believe that with the right analysis these questions can be answered quantitatively, so that the intuitive notion of “we need to take risk” can be turned into a definite answer to “how much risk, exactly, should we take?”.

* Footnote

An underdog needs to increase the variance of its final score.  Given that fact, it’s really tempting to think that the solution is for underdog teams to bring in “streaky” players.  If you’re down by 20 points, it seems, it’s worth rolling the dice with an unpredictable scorer who might get hot and go 17/20 from the field or might stink up the court and go 4/20.  (If you’re a Timberwolves fan, this person is Michael Beasley.)

The problem is that  statisticians have found absolutely no evidence for such players.  As far as a large number of advanced statistical methods can tell, the shooting patterns of every NBA player are consistent with the idea that all shots are statistically independent of each other.  There are no hot hands.

If this is true, then there is a strict relationship between the team’s shooting percentage and the variance of its final score.  Namely,

.

So apparently in basketball the only control a team has over their variance is through the value of the shot they are taking (a 2 or a 3).

Football, on the other hand, may be an entirely different matter, since there is a huge range of “values” for different plays.  It’s unfortunate, in that sense, that I grew up a basketball fan.  Assessing risk in football might be a much more interesting problem.

UPDATE: Since writing this post, its main idea has evolved to become a talk at the Sloan Sports Analytics Conference and a full-length paper (also available on the arXiv).