Feynman’s Ratchet and the perpetual motion gambling scheme
Can you spot a perpetual motion machine when you see one?
In physics, that question is equivalent to “can you spot a scam when you see one?”. That’s because a perpetual motion machine is, by definition, a fraud. It is a device that claims to generate useful work in a way that violates one of the most basic laws of physics: the laws of thermodynamics. The laws of thermodynamics are extremely fundamental to physics; they belong to a set of five or so ideas that can really be called “laws”, upon which the rest of physics is built.
So if you (portrayed below by Lisa Simpson) submit an idea or invention to the physics community (portrayed by Homer Simpson) that violates one of the laws of thermodynamics, you’re opening yourself up to a world of ridicule.
If someone tells you “what you’re proposing is a perpetual motion machine” (they’ll say perpetuum mobile if they’re trying to sound snooty), they might as well be saying “you couldn’t tell a Lagrangian from a lawnmower”. It’s a pretty strong rebuke.
In my experience, though, most physics students have a false sense of confidence in their own ability to spot a perpetual motion machine. They think that such a whimsical contraption will have an obvious, glaring flaw that’s easy to notice because it will violate energy conservation. “Oh, you forgot to take into account friction,” they’ll say, and then they’ll give you a short lecture on the First Law of thermodynamics. “Energy is neither created nor destroyed,” they’ll say.
The truth, however, is that most perpetual motion machines that you are likely to encounter do not violate energy conservation. Rather, the tricky and persistent scientific “scams” violate the much more nebulous Second Law of Thermodynamics, which says (in one of its formulations):
It is impossible for a device to receive heat from a single reservoir and do a net amount of work.
It is much easier to be fooled by proposals which violate this Second Law, which ultimately has its roots in probability rather than in the deterministic notions of energy conservation. In my life I have been fooled on two noteworthy occasions by seemingly good ideas that violate the Second Law of Thermodynamics. One idea was for a hypothetical machine to generate energy from thin air (molecules). The other was a sure-fire gambling method. In this post I’ll discuss both of these fraudulent schemes and why they fail, and I’ll try to explain why the Second Law of Thermodynamics can be stated like this:
It is impossible to profit, in the long run, from a truly random process.
The remainder of this post is organized thusly: First, I’ll introduce you to Feynman’s ratchet, a fairly popular thought experiment that seemingly yields a perpetual motion machine. I won’t tell you why it fails, though, until later. In the second section I’ll introduce you to an idea that I once thought could make me a rich gambler and I’ll explain why it doesn’t work. Finally I’ll come back to Feynman’s ratchet and explain why it also must fail for a very similar reason.
Feynman’s Ratchet
Imagine that you manage to construct the following device. You take a very small, very light-weight metal rod and attach some thin, paddle-like fins to one end. Let’s say that the rod is held in place by some low-friction bearing which allows it to rotate on its axis. If the rod/fins are sufficiently light-weight, then when they are exposed to randomly-moving air molecules some of these molecules can hit the fins and cause the rod to rotate in one direction or the other. You, the inventor, are hoping to harness some of this rotation in a useful way, but you need the rod to rotate consistently in one direction before you can do anything with it. So you attach the other end of the rod to a ratchet mechanism: a saw-toothed gear that interlocks with a spring-loaded lever (called a pawl). Like this:
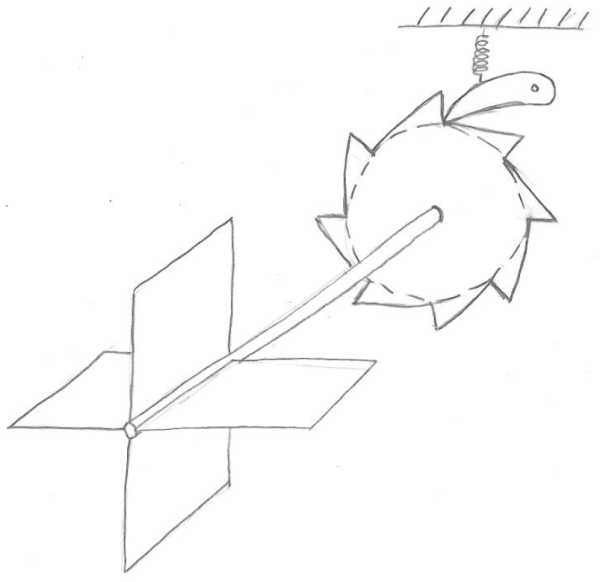 The ratchet, according to your design, will allow the rod to rotate easily in one direction (counterclockwise) but will not let it rotate in the other direction (clockwise).
The ratchet, according to your design, will allow the rod to rotate easily in one direction (counterclockwise) but will not let it rotate in the other direction (clockwise).
So there you have it. A simple perpetual motion machine. As long as the surrounding air molecules continue to move randomly, the ratchet should continue to spin (perhaps sporadically) in the counterclockwise direction, driven by occasional collisions with high-energy air molecules. You can even get useful work out of the ratchet if you want, for example by winding up a rope that lifts a small mass or by using the rod to drive a tiny electrical generator.
This clever thought experiment is generally known as “Feynman’s Ratchet”. It was popularized by Richard Feynman in his Lectures on Physics, although the original explanation belongs to Smoluchowski (of diffusion law fame) in 1912. I first heard of it as a riddle passed around by undergraduate students.
It’s not immediately obvious that such a machine should be impossible. It certainly doesn’t violate energy conservation, nor does it rely on any “zero friction” assumptions. Feynman’s ratchet gradually uses up the energy of the randomly-moving air molecules around it (cooling the air as it gains energy through collisions), but so long as the earth is heated by the sun it should continue to rotate and, seemingly, provide useful work. It seemed to me, as an undergraduate, that this was a clever little device for converting solar energy to useful work.
But, by decree of thermodynamics, Feynman’s ratchet cannot work as a heat engine. It plainly violates the Second Law, which says that useful work can only be obtained by the flow of energy from high to low temperature. This device purports to get energy from a single temperature reservoir: that of the air around it.
Where does it go wrong?
If you’re encountering this riddle for the first time, you can try and figure it out for yourself before I tell you the answer below. But it may help you to first consider another bogus scheme, which I stumbled upon as a high school student and thought for sure could make someone a fortune.
The perpetual motion gambling scheme
It was during high school that my nerdy friends and I first discovered the joys of computer programming. It seemed to me then (and still seems now) a remarkable form of instant gratification: if you want to see what happens in a particular hypothetical situation, you just ask the computer to work it out for you and you get to avoid a lot of tedious and questionable theorizing. Of course, the marvelousness of the computer can quickly lead to the programmer developing an over-reliance on its powers, and from there it’s easy to fall into a kind of intellectual laziness that gets you into all kinds of (scientific) trouble. It’s probably this computer-born laziness that first allowed me to be fooled by the “perpetual motion gambling scheme”.
Back in 11th grade, the programming platform of choice for my friends and I was the TI-83 graphing calculator. Our setting of choice was the back of physics class. On one particular day, I was playing a simple blackjack program that my friend had made when I discovered that I could make money every single time I played. What’s more, I could make an arbitrarily large amount of money, apparently only by judiciously deciding how much to bet at each hand. I only learned much later in life that I had stumbled across a system called the “martingale strategy“. And only very recently did I realize that hoping to profit from the martingale strategy amounts to a perpetual motion machine, and is in violation of the Second Law.
If you’re unfamiliar with the martingale strategy, it goes as follows. Consider the simplest possible gambling game (you can easily generalize to other games, like blackjack): you place a bet and then flip a coin. If the coin comes up tails, then you lose all the money you bet. If the coin comes up heads, then the money you bet is doubled and given back to you. It’s a completely fair game which, on average, should give you zero net profit. The martingale strategy is to place an initial bet (say, $1), and then double your bet each time you lose. In this way a victory at any given coin toss will completely compensate for all previous losses and give you a net profit of $1. In flowchart form, it looks like this:
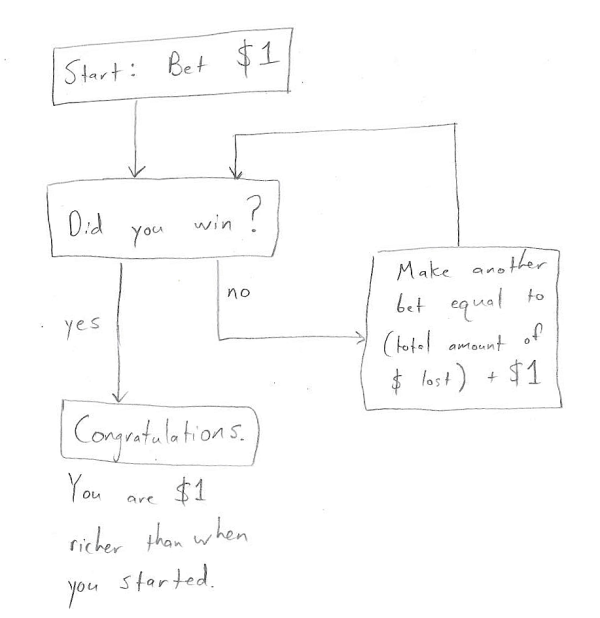 Notice that there’s no exit to this flow chart except at “Congratulations”. You can’t lose!
Notice that there’s no exit to this flow chart except at “Congratulations”. You can’t lose!
Of course, it’s possible that you, the bettor, only have a finite amount of money to bet, which would imply another ignominious exit to this flow chart corresponding to “you have completely run out of money”. (This was impossible in my friend’s TI-83 blackjack program, which allowed you to go into arbitrarily large amounts of debt). But the finiteness of a person’s funds didn’t seem like an insurmountable problem to me.
Here’s how the strategy played out in my high school student imagination. Come to the gambling table with some unthinkably huge amount of money: say, dollars. Now follow the martingale system until you reach a profit. The only way the system could fail is in the extremely unlikely event that the coin comes up tails ten consecutive times. The probability of that happening is only
, so, I reasoned, it can be ignored. Once you’ve followed the chart and won your $1, start over by resetting your bet to $1. Repeat the system ad nauseum until you’ve made all the money you want. Go home rich and happy.
And, of course, the strategy is very flexible. If you’re richer than my “unthinkable” thousandaire and you’re not content with a 1-in-1000 chance of losing, then you can start by coming to the table with dollars, which would imply a tiny
chance of failure. Or if you want to make money faster (with slightly higher risk), then at each coin toss you could bet (total amount of money lost) + $10 instead of + $1. What could go wrong?
What could go wrong, of course, is the Second Law of thermodynamics. It says (in my formulation) “you cannot profit from a random process.” Long-time readers of this blog (thanks!) may notice that the martingale system sounds suspiciously similar to Matt Ridley‘s strategy for biasing the gender distribution: keep having children until you have a boy, and then stop. It didn’t work there for the same reason that it doesn’t work here: a truly random process cannot be used for directed motion.
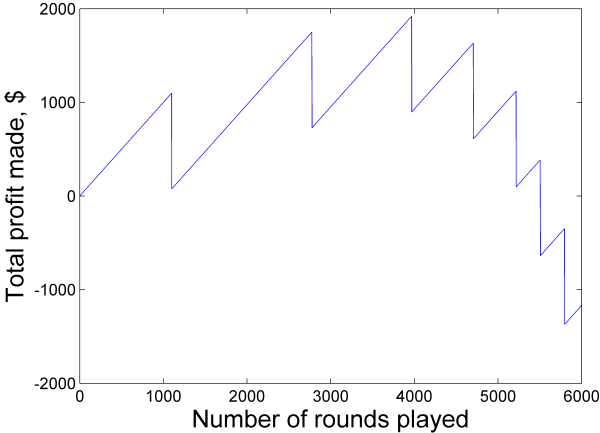
And, actually, the martingale system isn’t too hard to pick apart once you stop being analytically lazy (as I was in high school) and actually weigh the different outcomes. Take the example where I come to the gaming table with dollars and follow the strategy from the flowchart above. Then 1023 out of every 1024 games my strategy will succeed, and I’ll receive as my prize $1. However, once in every 1024 games the strategy will fail, and when it fails it will fail spectacularly: I’ll lose $1023. So if I keep playing the game long enough, on the whole I will make zero profit.
Just to make the point visually, here is a simulated string of “martingale” rounds, showing one possible evolution of the gambler’s net profit over time.
Note that at a given round, your profit is almost certainly increasing (positive slope), which is why the martingale strategy is so alluring. If you start from zero, then you will most likely earn some money in the short term. But given enough time, those big drops will hit you and you will find the strategy unprofitable.
Let me say this more again explicitly, as a hint to those still thinking about Feynman’s ratchet. You cannot get directed motion out of a random process. You can set up a system that makes a step in one direction (profit) more likely than a step in the other direction (loss), but it will always be accompanied by a change in the size of those steps so that on the whole you go nowhere.
Got it?
Feynman’s ratchet is explained after the jump
The downfall of Feynman’s ratchet
The problem with Feynman’s ratchet, as you’ve probably figured out by now, is that there is no such thing as a perfect ratchet mechanism. What I drew above was a spring-loaded lever that is supposed to prevent the gear from rotating backward. But in a thermal environment, where energy can be absorbed from randomly-moving air molecules, nothing is impossible. Things only become improbable due to the high energy they require.
So it must be possible for the gear to rotate backwards (clockwise). In this case, it requires a strong collision from some air molecules against the lever, so that the lever gets pushed up and past the tooth of the gear and the gear can slip backward. There is a corresponding small rate at which the gear skips backward by one tooth (so that the lever snaps into place in a new location).
Of course, this backwards rotation is much less probable than a small forward rotation. But consider that for the gear to rotate forward by one tooth, a whole bunch of small rotations must be chained together consecutively. The net rate of all of those small rotations coming together is also be fairly small.
And, in fact, the Second Law guarantees that the rates of a forward rotation and a backward rotation are the same. It seems surprising that this should be the case, no matter how carefully the ratchet is designed and no matter what size/shape the various pieces are. But it is. In the Lectures on Physics, Feynman estimates the rates of these two processes and shows that they are, in fact, equal (Chapter 46).
Of course, if you really wanted to make the machine work you could cool down the air on the ratchet side or heat up the air on the fin side, like this:
But in this case, you’ve only managed to generate work in the same way as a common steam engine: by creating a temperature difference and then using some of the heat that flows from hot to cold. (Here you’ll need a heat pump to prevent the temperature from equilibrating with
by conduction along the metal rod).
What did we learn?
And now, like a good episode of G. I. Joe, this post concludes with a recap of the morals to be taken from it. The first moral is the Second Law itself: it is impossible to extract directed motion from a random process (a single heat reservoir). Anyone who claims they can do so is either mistaken or a charlatan.
A perhaps equally important lesson, though, is that it is easy to be fooled when it comes to the laws of thermodynamics. In the last decade or two, for example, there was much controversy over the mechanism by which muscle fibers contracted, before someone realized that one of the leading proposals amounted to a perpetual motion machine.
So be aware. Because knowing is half the battle.

Awesome post! I frickin’ love your blog 🙂
Thanks, Erin. I wish the posts came more often, but they generally take me about 8 – 10 hours each to write so I tend to put them off. My “things to blog about” list is growing pretty long!
Fantastic stuff, again! A university, and their students, is going to get very lucky when you graduate (or after a postdoc, as necessary).
Not to add to your list of things to do, but a twitter/facebook link, maybe even a facebook fan page, might be helpful. More people should see your outreach work.
Thanks shane. I don’t think I have the ego to make a fan page for myself, but your other suggestions are probably a good idea. I think I just successfully added a twitter/facebook “share” link. Let me know if it doesn’t work.
Yep, it works. Nice. I look forward to your next installment, as always.
How does a windmill work then? Does it work under the same principle as the ratchet? The windmill only pumps water upward out of the ground, not down, and relies upon air movement. Do windmills only work where the wind mostly blows in one direction and not randomly? What if a fluid flows randomly in opposite directions? Can energy by extracted to perform useful work, such as pumping water upward? Your post needs further explanation.
A windmill works, ultimately, by exploiting temperature differences that produce gradients in air pressure. Hot temperatures create higher air pressure while cold temperatures produce low air pressure. Wind is the process of moving the thermal energy of air molecules from high to low temperature/pressure. A windmill exploits this motion (which is not random, as you suggested, but has an overall drift) in a way that is allowed by the Second Law.
Well,the law of entropy says that temperaratures and pressures ,after doing work decay and increase the entropy of the system and tend to make them uniform or equal at everypoint.Consider the pressures in the atmosphere and the occeans which depend only on gravity which will never allow the pressures to become equal at every point on a vertical line.How to explain?
Hi antripathy.
You have to be a little careful with how you’re stating the second law. The second law says that the entropy of a closed system will become uniform over time (i.e. the pressure and density will be equal everywhere). A box of gas molecules, for example, when isolated from the rest of the world will eventually equilibrate completely so that its pressure is uniform.
If you have a column of water interacting with a gravitational field, however, that doesn’t constitute a closed system. There is still some large mass outside the system pulling on the water molecules and causing them to arrange in a way that prefers higher pressure at lower altitudes.
A more correct principle for this system is that the chemical potential is uniform. This is the average free energy per water molecule: energy minus temperature times entropy.
It is impossible to profit, in the long run, from a truly random process.
I’m not sure this is the best way to summarize your observations. Say I invent a game where we flip a fair coin, and every time it comes up heads, I give you $5. It seems like you profit, in the long run, from a truly random process.
Also, what about this article: (http://www.telegraph.co.uk/finance/personalfinance/consumertips/8185280/Is-this-a-bet-you-cant-lose.html). It says that some people are finding surefire ways to profit from betting on horses because sometimes bookies give away free bets. Are we to conclude from this that horse racing isn’t random (over the long term)?
Good point. I guess a better statement would be “It is impossible to profit, in the long run, from an unbiased random process.” Here, “unbiased” means “zero expectation value. Your hypothetical game has an expectation value of $2.50, so of course you will profit in the long run.
Coincidentally, this is why it is possible to make a profit from the stock market. There is a net upward drift in the total stock market value due to the world becoming more efficient at producing goods and services. Of course, there is the fact that that stock market isn’t “truly random”: you can make use of knowledge about the company to weigh the probabilities.
As for your article, it seems to me that the crux of the “sure fire” method is in taking advantage of incentives offered to first-time bettors. It looks like certain bookies have found it profitable to unbalance the odds for first-time users (so that users win, on average) in order to get people hooked on using their gambling service. I don’t know if the scheme reported in the article works, but if it does then it’s based on quickly jumping from one service to another and taking advantage of their “one time” offers. In that sense it’s a little bit like signing up for one of those “get 12 cd’s for 1 cent!” subscriptions and then canceling immediately. Again, the Second Law remains intact. : )
Your restatement of the second law of thermodynamics as “impossible to profit, in the long run, from a truly random process” is incorrect. Blackjack is random and it is possible to profit in the long rug by card-counting.
By counting cards you’re removing the randomness.
You’re not removing the randomness. The cards are no more ordered than they were before simply because you made some predictions about the order in which they would turn up. Does making weather forecasts that turn out to be correct more often than not remove randomness from the weather?
I don’t buy his reply about windmills either. Windmills I have seen are made so that they pivot vertically to always face toward the wind. Thus, windmills are able to generate work from wind that blows from random directions.
What if am in a sail boat and I want to cross a lake where the wind blows randomly? When the wind is blowing in the right direction I put up my sail. When the wind isn’t favorable, I reef my sail and anchor. Eventually, I will be able to cross the lake by exploiting the wind even though it blows in random directions.
I like your sailboat question a lot. It’s a tricky one!
My guess at a solution is this:
First let me imagine that the sailboat and the lake are in complete isolation (i.e. not sitting in the middle of a big, externally-imposed air temperature/pressure gradient), so that the wind truly is “blowing randomly”. It does seem possible that you could cross the lake by (very quickly) raising and lowering the sail at the appropriate moments.
But then the problem is exactly like the problem of Maxwell’s demon ( http://en.wikipedia.org/wiki/Maxwell%27s_demon ), which says (in this case) that you might be able to move your sailboat from one side to the other, but you are going to expend a lot of metabolic energy raising and lowering the sail. So by the time you’ve managed to cross the lake, you’ve spent enough energy that you’ve essentially moved the boat by the process of transferring energy from a high-temperature source (yourself) to a low temperature source (the surrounding air). It’s the same as if you had just paddled the boat, which doesn’t violate any laws of thermodynamics. While you used the random air molecules to get across the lake, they’re not ultimately the driving force behind your motion.
You might think that you could just concoct some automated (ratchet) system to raise and lower the sail by itself. But I can guarantee, by the second law, that this system will either require a fuel source or it will fail. The same way that your swiveling windmill example will fail unless it has some energy input (e.g. a gas-powered engine) or exploits external temperature gradients.
In your Martingale example, what about the other party to the bets, the casino or the person with the deep pockets that accepts every bet? They make money from the random process. Maybe your restatement should be “[i]t is impossible to profit, in the long run, from a truly random process UNLESS YOU HAVE FIGURED OUT WAY TO PROFIT FROM THE RANDOM PROCESS.”
The casino actually doesn’t make money in this example. If the game is fair (zero expectation value), then everyone gains nothing on average.
Wrong. The casino wins because it has a much larger bank roll. Review the part about “you only have a finite amount of money to bet”.
I think that, in a “real” game in a casino, the casino actually makes money not so much because it has a bigger bank roll but because the game is biased in its favor. I’m afraid I’m not that much of a gambling expert but I am pretty sure that this is the case, in terms of odds versus payouts, for roulette, craps, etc. It is notably *not* the case for blackjack, because as you pointed out above, it is possible to skillfully count cards to make money versus the house when playing blackjack. In *that* case, I believe that the advantage you have is not that you have outwitted a random process, but that the house is required to play by a set of fixed rules (hit on 16, stay on 17, or whatever the actual requirement is), and is not allowed to *itself* count cards to follow an optimum strategy.
“It is impossible to profit, in the long run, from a truly random process.” Seems applicable to explain the faulty premises that belied the trading practices of the “quant jocks” which led to the financial meltdown of 2008? They seemed to have not considered that 1 out of 1024 times their assumptions wouldn’t work! Perhaps they were with you in the back of that physics class playing blackjack on that old TI-83? Curious if think there’s any merit to my conjecture? Love the blog!
Thing is — I can’t help thinking as the statistician that I am. Presumably all of this depends on the distribution of the random air movements. The reasoning seems to rely on a fat tail — i.e. a non-trivial probability of a large swing. Yet it seems equally possible that large swings are EXTREMELY unlikely. I find it hard to believe that there is no hidden assumption there.
The kinetic energies of the air molecules follow the Boltzmann distribution: they are distributed according to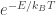 . So the “fatness” of the distribution depends only on the temperature, and the argument above works for all temperatures.
. So the “fatness” of the distribution depends only on the temperature, and the argument above works for all temperatures.
Really, though, all you need to know is that the rate at which a given thing happens depends only on how much energy is required to make it happen. In this case, the ratchet swings backward and forward at equal rates because it takes the same amount of energy to move over one of the teeth forward as to move over it backward (you have to lift the lever one tooth-height either way). The only difference is that the gear can rotate a little bit forward (which requires a small amount of energy) without clearing the edge of one tooth, and then the spring-loaded lever will push the gear back until the lever is at the bottom of the tooth again. On the other hand, if the lever happens to jump up and the gear rotates by only a tiny amount, then the lever will push the gear backwards until the lever rests at the bottom of the preceding tooth.
You should also remember that uniform temperature implies that everything in the environment follows the same Boltzmann distribution. So the air molecules and the atoms that make up the ratchet itself are all randomly kicking around. In this way all possible motions by all objects are being explored simultaneously, and any given motion occurs at a rate dependent only on how much energy it requires.
Thanks for the impressive post. It clarified many issues and, as it is probably supposed to be, suggest new ones…:-)
Here’s my thought experiments that apparently violates the second law. Not a very original one, but still I cannot see where it breaks down.
Imagine you have a very thin and tiny whisker (what in scanning probe microscopy is usually called a cantilever). It is clamped at one end and free to move at the other. The system is at room temperature.
The whisker will vibrate at its resonance frequency around the equilibrium position just for the fact that it is at a finite temperature. Above the whisker you have some kind of traducing system: to simplify things just imagine that the vibrating sting hits something and then transfer to it some of its mechanical energy.
This “hitting something” will damp a little the vibration, but the thermal bath is providing constantly thermal energy so we will still be in steady state. Maybe it’s a different steady state than if the sting would be freely vibrating, but it’s still a steady state.
Am I not getting mechanical energy out of one single thermal bath or, if you prefer, out of a truly random process?
What if the saw-toothed gear and the ratchet are in a vacuum?
The vacuum wouldn´t do so much, since the tiny pawl will anyhow bounce up and down due to thermal motion — even if it´s not hit by particles. (So, the system will even rotate in opposite direction if the temperature T2 is higher than T1…)
But how about this one: Consider the ratchet being built high above the fins, so that because of gravity T2 became lower than T1. It should work then, wouldn´t it? Anyhow, these temperature differences might be far too small to have a noteworthy effect…
Very nice blog btw, thanks very much!
yeah, this seems wrong, the ratchet is powered by wind, which is powered by the sun, which is hardly perpetual energy, the ratchet mechanism just acts to filter out undesired forces. A ratchet that slips backwards is most likely broken, and it’s very hard to break a steel tool by blowing on it.