Braess’s Paradox and “The Ewing Theory”
I spend a silly amount of time thinking about basketball. Usually this works directly to my detriment, since it means that I easily get distracted when I’m supposed to be working. And when you’re trying to make living “theorizing”, focus can be at a premium. But after Tuesday’s post on the price of anarchy, I can’t help thinking about what these ideas could do if they were applied to basketball. If you haven’t read the “price of anarchy” post yet, please do, or the things I say here might not make a lot of sense.
Like the study of traffic patterns, basketball is a network problem. Each possession can be thought of as a journey from point A to point B, where point A is the beginning of the possession and point B is a shot attempt. The team can go from A to B by any number of routes. The “path” they take is the sequence of plays and passes leading up to the shot. As a simple example, here’s what a pick and roll between the point guard and the power forward might look like: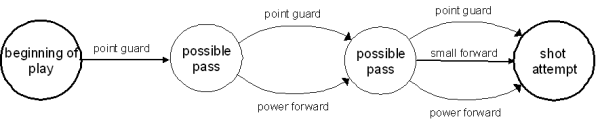
One possible outcome of the play is that the point guard keeps the ball the whole time and takes a shot: this would be the top routes. You could also have the point guard pass to the power forward after the screen and have the power forward take the shot: this would be the bottom routes. Or you could have the point guard pass to the power forward after the screen, who then hits the cutting small forward for the shot. Each of these plays (there are six possibilities) represents a different path, and each path will have a different efficiency.
If you’re a basketball coach or player, the question you want to know is: which plays should I run, and how often? In network language, the question would be: what is the optimal usage rate for each path? The question can be an extremely tricky one, as we saw with traffic patterns. It may be that shutting down a link or a node (elminating a possible pass or player from the play) improves the overall efficiency. In the study of traffic, this was Braess’s Paradox: closing a road can improve traffic. In basketball, it gets called “The Ewing Theory”, and its implication is this: eliminating a scoring option can improve the efficiency of your offense.
If you’ve never heard of The Ewing Theory, please check out this article by the always-hilarious Bill Simmons of ESPN.com. Simmons coined the term to describe the observation that the New York Knicks always seemed to play better when their best player, Patrick Ewing, was out. (Just to be pedantic, the “Ewing Theory” isn’t really a theory; it’s an observation. It should probably be called the “Ewing Paradox”).
My goal for this post is to give a plausibility argument for the Ewing Theory. I want to show that it is truly possible for a team to improve when their best player and primary offensive option is removed. What’s more, it can happen without any psychological effects (like the team being extra motivated to play hard without their star player). The answer has everything to do with the price of anarchy, and the fact that making the highest-percentage play every time down the court is not the same as playing your best possible game.
The team with a dominant big man
Basketball may be a network problem, but it is an almost hopelessly complicated one. There are so many possible variations of so many possible plays, that it would be silly to try and draw them all out in one diagram. So I’m going to simplify the network very drastically, and assume there are only two points: the beginning of the possession and the shot attempt. This is equivalent to assuming that the only thing that matters for efficiency of a play is who takes the shot. It’s a big assumption, but it allows us to make definite predictions. I’m going to assume that the team has one star player, whom I’ll call Patrick, and four “average” players. The diagram for their offense will look like this:
Patrick may be far-and-away the best offensive option on this team, but that doesn’t mean that he should shoot every time. That’s because, as a scorer, he will become less efficient the more he is used. The more shots Patrick takes, the more the defenses will focus on him and make it hard for him to score. As a result, Patrick’s teammates should take some significant fraction of the team’s shots, even though they are not as good as he is. We can make a guess as to how Patrick’s offensive efficiency might decline with the number of shots he takes:
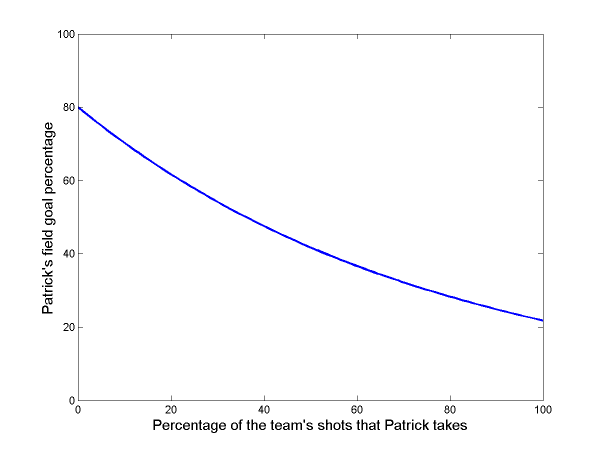
This graph, of course, is just a guess. But its main features are important
If Patrick is used only very rarely, then the defense will not adjust to him and scoring will come easy. As a result, he’ll shoot nearly 80% from the field. In contrast, if Patrick takes every shot his shooting percentage will drop to nearly 20%.
It’s not terribly easy to find justification for this assumption: a good player never takes only 2% of his team’s shots, and no one in their right mind would ever try to take every single shot for his team (*insert Allen Iverson joke here*). But there is definitely evidence for a negative correlation between a player’s field goal percentage and the number of shots he takes. Consider this data for “dominant big men” Shaquille O’Neal and Kevin Garnett:
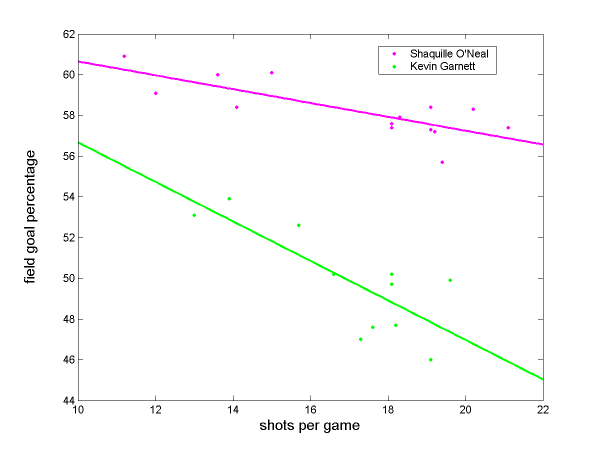Each data point on this graph represents a different season in their respective careers (see Data Footnotes at the bottom). The message is fairly clear: when your big man is used as the primary offensive option, his efficiency suffers. When he is used more rarely, to clean up misses and take advantage of low-post mismatches, he is significantly more effective.
Just to show that this effect isn’t limited to low-post players, here is a similar data set for guards Ray Allen and Kobe Bryant:
Clearly, Ray Allen the occasional sharpshooter is more effective than Ray Allen the go-to offensive creator. And the story is similar for Kobe Bryant.
How to best use your superstar
Back to our hypothetical Patrick. Suppose that Patrick’s “average” teammates all shoot 45%. (Since none of them will ever be called upon for more than a fifth of the team’s offense, we don’t need to worry about how their efficiency declines with usage.) Patrick is clearly a better shooter than his teammates, so how many of his team’s shots should he take?
The answer depends on your level of strategy. You might think that the best option is to feed the ball to Patrick until his field goal percentage drops to the level of his teammates. Only then should his teammates shoot the ball. And indeed, it’s hard to argue with this logic: if Patrick is shooting 60% and his teammates are only shooting 45%, then clearly Patrick should be taking more shots, right? In game theory, this strategy is called the “Nash Equilibrium”; it is the result of considering each play individually, and looking for the best possible outcome. It is also completely equivalent to the “selfish” optimum in the traffic problem, where each driver takes the path that is in their own best interest. As a result of the strategy, Patrick takes about 44% of the team’s shots (more than three times more than any of his teammates) and the team shoots 45% from the field.
But something seems wrong, doesn’t it? You have a superstar player who is capable of shooting as well as 80% from the field, but still the team is only making 45% of its attempts? There must be a better strategy. And, of course, there is. Here is a plot of the team’s overall shooting percentage as a function of the number of shots that Patrick takes:
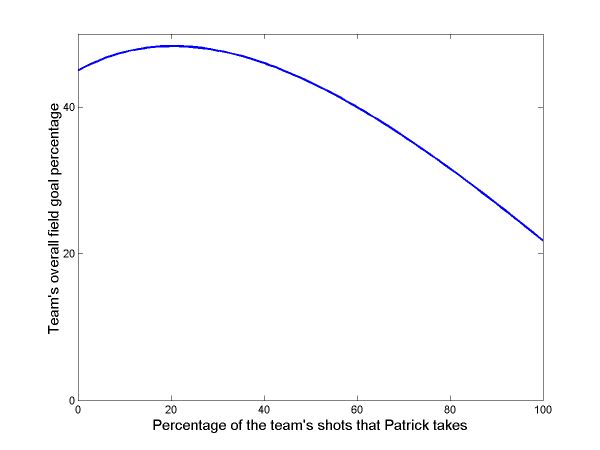As you can see, the team is most efficient when Patrick takes only about 21% of the team’s shots, just slightly more than everyone else. It seems ridiculous at first: in such a game Patrick would be shooting 60% while his teammates shot only 45%; surely he should be getting more shots. But the added benefit of keeping Patrick more poorly-defended pays off, and his team’s shooting percentage improves to about 48.5%.
This is the price of anarchy in basketball. A team that looks for the best play each time down the floor will shoot only 45%, whereas a team aware of its “global optimum” can do as well as 48.5%. They just have to purposefully refrain from going to their superstar, even when he is the best option.
I think about this sometimes when I watch the Magic use Dwight Howard sparingly, or when the Lakers use Pau Gasol only as a third option, even though he’s clearly their most efficient scorer. Maybe that’s not bad teamwork; maybe it’s good strategy.
What happens when Patrick goes out?
So what happens when Patrick injures his Achilles tendon and must be replaced by an “average” teammate? Certainly, the global optimum decreases. The team no longer has Patrick’s 60% shooting to bolster them, and must rely on a team of five 45% shooters. But if the team was going by the “one play at a time” strategy (the Nash Equilibrium) and not the best possible strategy (the global optimum), then losing Patrick doesn’t hurt them at all. Having five equally “average” players forces them to share the ball and prevents the defense from focusing in on any on player. As a result everyone shoots 45%. They shot 45% when Patrick was on the court anyway, so the team loses nothing by having him sit out.
The arguments of this post have been a little tricky, but the final conclusion is fairly straightforward. When the team’s best player is not on the court, the team is forced to make harder, lower-percentage plays and to share the ball. And when a team shares better, it plays better: the defense is kept off balance and has no room to focus in on any one guy. These sorts of improvements can make up for the loss of direct offensive production.
The point of this post was not to make a quantitative prediction. There were a lot of unjustified assumptions here, and you shouldn’t take any of them too literally. The point was to show that the “network” of an offense can have surprising and unpredictable properties. For a team to play its best possible game, it might need to intentionally take lower-percentage shots. When a team loses a high-percentage option, its overall offense might adjust in surprising ways that can make the team better. Flow becomes re-routed in the offensive network, and the result might be to push the team closer to its true global optimum. The Ewing Theory, in my mind, is completely plausible.
Data Footnotes
- The data above is taken for full seasons from the careers of the respective NBA players. I omitted the first two seasons of each player’s career (while they were still improving significantly), and any season where the player missed more than a third of the games due to injury.
- Kobe Bryant had two seasons of anomalously low field goal percentage during the rocky seasons of 03-04 and 04-05 (where he missed 33 games because of the Colorado rape trial and a severe ankle sprain). These are shown on the graph but are not included in the fit line.
UPDATE: To those readers who objected to my use of FG% as a measure of “scoring effectiveness” rather than something like TS%, maybe this will be slightly more convincing:
http://i1012.photobucket.com/albums/af249/gravityandlevity/skill_curves-1.png
The open circles/squares represent the first three years of the players’ careers.
UPDATE #2: A more detailed example of Braess’s Paradox in basketball.
Trackbacks
- Rush hour traffic and the price of anarchy « Gravity and Levity
- “Like the study of traffic patterns, basketball is a network problem.” « Found Connections
- Etl World News | Assorted links
- "Ewing Theory" article
- Assorted links « See the Invisible Hand Blog
- The 10-man rotation, starring the NBA national TV schedule | ReadSports.com - Your primary source for all sporting news
- An example of Braess’s Paradox in basketball « Gravity and Levity
- Good news from the Sloan Sports Analytics Conference « Gravity and Levity
- Friday Links « Open Economics
- Monday Medley « No Pun Intended
- America + Football = Progress? | Thomas the Think Engine
- Risk is the ally of the underdog « Gravity and Levity
- Rush The Court » Blog Archive » Alpha Dogs, Traffic Jams, and Derrick Williams
- Video scouting: Rudy Gay
- When is a shot too good to pass up? — The shooter’s sequence « Gravity and Levity
- Stretching the Game Out: The Pantheon of NBA Writing on the Internet | The Gothic Ginobili
- Zero Gravity (and Levity) « Gravity and Levity
- What we know about the theory of optimal strategy in basketball | Gravity and Levity
- “They’re definitely not a better team, but they’re harder to guard” - examining the juxtaposition of the Warriors without Durant - NBA NEWS 24
Gravity and Levity 
Think about teams that are centered around one “star” player and when he scores 40+ his team has a losing record.
It does happen.
Every time Lebron James plays the Magic…
Just wanted to say that I love reading your sports articles. Keep ’em coming!!
Thanks! It’s funny; I started this as a physics blog, but my sports-related posts end up getting most of the traffic.
Because no team has four equal players, doesn’t this imply that a team should play its five worst players?
The short answer is no, but the long answer is a little more complicated.
In the simplistic description I’m using here, there are two ways of characterizing how good a player is:
1) His shooting percentage when he takes very few shots
2) The rate at which his shooting percentage declines with increased number of shots.
When people say that Kobe Bryant is the best player in the NBA, they are generally implicitly using the second characteristic. (Hard defense has a smaller effect on him than on most people). But he is still pretty inefficient compared to someone like Tyson Chandler.
If player B is worse than player A by both of these rankings, then the team should always be worse when A is replaced by B. But if B is worse than A in only one of the two, then it may be that the replacement causes the team to change their shot selection in a way that improves overall performance.
So it is possible that a team could replace Kobe Bryant with Tyson Chandler and do better, even though Kobe is clearly the better player. But it depends very much on which strategy they were using to play: a “global optimum” or a “Nash equilibrium” strategy.
It’d be interesting to see if the presence and play of star players ever elevates their teammates’ shooting percentages. I would not be surprised if having Kobe in the game (or perhaps the ideal example, Jordan) creates easier baskets for the rest of the team, and if so, if there is a point where this compensates for the star’s own declined shooting percentage?
I don’t believe that the relationship between shots attempted and field goal %age is linear- I would expect a curvilinear relationship where very few shots and many shots both exhibit a lower field goal percentage than a moderate level of shots- at least at the per-game level. Any optimizing regression model may need to take quadratic (or possibly cubic) relationships into account. Good article, very thought-provoking.
I’m sure you’re right that a simple linear relationship is inadequate to describe the skill curve over the full range (0% to 100% of the team’s shots taken). I only used a linear relationship as a first attempt, because any curve is linear when looked at over a small domain. I would expect that you need to take non-linear corrections into account when you that think a player’s shot fraction might take any value in a large interval: not just between 15% and 25%, but between, say, 5% and 50%.
hey great article!
🙂
Evan
Has the OP made the assumption that the 4 average players shooting percentage doesn’t vary with the number of shot attempts they have? I just don’t understand this idea, as the entire reason shooting percentage varies with attempts is defensive attention.
The reason Ewing’s percentage goes up if takes fewer shots is that the defense pays attention to the other players. Well, wouldn’t it stand to reason that if the other players face increased defensive attention (because Ewing is taking fewer shots) that the average players would face increased defensive attention? I mean, the players don’t either pay attention to Ewing or no one, right?
Hi Steve,
You’re right to object a little bit; the correct way to approach the problem is to take into account how all five players’ efficiency changes with their volume of shots. I was just trying to simplify the problem a little bit to make its main conclusion evident. Since Ewing was the only player whose number of shots was varying significantly, I just talked about his efficiency changing.
If the other four players have shot percentages that don’t change too drastically in the range 10% – 20% shots taken, (say .5 to .45), the story doesn’t change much. Although it makes the “price of anarchy” slightly smaller than I’m claiming here.
I may be misunderstanding the reasoning, but it seems to me that there’s no problem with dynamic Nash equilibrium here. Though Patrick is shooting 60% when taking 20% of the shots, his *marginal* make rate is very, very low – if he falls from 60% to 40% FG% when going from 20% to 40% of shots, then he’s making about 25% of the shots in that new interval. Without knowing the exact formula of Patrick’s curve, I can’t confirm this, but it seems to me self-evident that Patrick’s *marginal* FG% when taking 21% of his team’s shots will turn out to be 45%.
That is, I don’t see any paradox here, but merely a mistaken definition of the payoffs when looking for the Nash eq.
Kevin
Hi Kevin,
I think that we are thinking about that first graph differently. You seem to be thinking about it as “Patrick’s shooting percentage as a function of how many shots he takes over the course of the game.” I meant something more like “Patrick’s instantaneous shooting percentage as a function of his current shot usage.”
Your reasoning about marginal shot efficiency would suggest the following scenario: if Patrick shoots 100% of shots in the first quarter, but none in any subsequent quarters, than he has only taken 25% of his team’s shots and therefore will make almost 55% of them or so.
What I meant to imply was that if Patrick has generally been taking about 20% of his team’s shots during the course of the game, then his next shot has a 60% chance of going in. Under the scenario above, he should only have made about 20% of his shots.
So in that sense the graph is meant to describe marginal shot efficiency. This is something like a “continuum approximation” (assuming a very high density of plays), and it’s certainly questionable. But that was the idea I meant to convey.
I understand why the NE isn’t working, then. Patrick’s *marginal* decision to take one more shot, under this interpretation, also lowers his shooting percentage for all previous shots. The payoff functions still look very strange here, though. When his teammates are deciding, in NE, whether to pass once more to Patrick, they should realize not only that he has x% chance of making that shot, but also that his overall efficiency on future (and past, in this case) shots will fall.
I guess the assumption is that the “equilibration” happens rapidly, relative to the total length of the game.
The Nash Equilibrium, as I envision it, happens when Patrick’s teammates keep feeding him the ball until his efficiency is only as good as theirs. It’s true that his shots during this initial period of equilibration should count for something, and not be “lowered by his current decision”. But I’m making the assumption somehow that the equilibrium is reached quickly, so that there are only a few shots (4 or 5 out of 90?) taken “out of equilibrium”.
In real basketball terms, I think that your last statement is the real point I was trying to make with this post. Perhaps I used terms like “Nash Equilibrium” in a misleading way (forgive me; I have no formal economics training outside of high school). But the idea is that if Patrick’s teammates do not take into account how present shot selection decisions will affect future efficiency, then they will perform below the optimum. Even if their present decisions are perfectly well-informed, and always in their immediate best interest.
In the past, I too argued for declining marginal returns on shooting percentage, citing, for example, Wilt Chamberlain’s .506 field goal percentage in 1962 when scoring 50 ppg and .727 in in 1973, when scoring 13 ppg.
But, having wasted a lot of time recently looking through a basketball encyclopedia, I must say that evidence on a season to season basis for higher scoring average equals lower shooting percentage is nowhere near as strong as I thought. For example, there was a year in the late 1970s when the Houston Rockets lost Moses Malone and two other stars to injuries, so 5’9″ Calvin Murphy ended up taking a huge number of shots as the team’s #1 option — and Murphy wound up shooting about the same percentage as his surrounding seasons.
I think the more interesting question is why we don’t see the kind of routine diminishing returns on a seasonal basis that both of us expected in theory. (Perhaps minor injuries play a role …)
The more Michael Jordan shot the ball the more he was guarded. The difference between him and Patrick Ewing is that he got better when it happened.
I think the logic of the argument is sound. Think of each possession as a car. Say there are five possessions. Consider this table:
Patrick Team
Shoots Expected Points
0 2.25
1 2.41
2 2.33
3 1.98
4 1.57
5 1.05
Clearly, to maximize the team’s expected points, Patrick should shoot only once out of the five times. If Patrick doesn’t shoot at all, the team shoots 45% and so 5 times 0.45 is 2.25. If Patrick shoots once (taking 20%of the shots), he shoots 61%, so we compute expected points as 1*0.61+ 4*0.45 = 2.41. If Patrick shoots twice, it’s 2*0.49+3*0.45 = 2.33. (The rest of the table doesn’t matter really, but Patrick’s percentages are 36%, 28% and 21% if you want to crunch the numbers. I used % = 0.8e^((-4/3)% shots taken).)
With these concrete numbers, we can really figure out what’s going on. The key is in the decrease in expected points from Patrick taking 2 shots instead of 1. How can expected points fall since his % when taking 2 shots is 49% and this is higher than 45%? Look at the table again. Patrick shooting twice is better than him never shooting, but it’s *even better* if he only shoots once. When he takes that second shot the fall in his % from 61% to 49% is so harmful to the team that it lowers expected points from its maximum. I think that’s the key — lowers expected points from its maximum, NOT FROM 45%.
The comments to the original post on “marginal” are directly related to this. You can solve this problem with calculus by setting the derivative of the expected points function equal to zero. If you do that, you’ll reveal a marginal condition where the additional (not average) points from one more shot by Patrick have to equal zero. BTW, with the function above, I got that Patrick should shoot 20%, not 21%. Maybe my function is a little different than yours?
Now I’d like to make a basketball point that has thus far gone unnoticed. Unlike the cars example where each driver makes his or her own decision and fails to incorporate the full cost of that decision, leading to a suboptimal allocation (aka too much congestion), a basketball *team* is not five separate players making individual decisions. If it was, Patrick would shoot too much and he’d have a 45% shooting percentage. The point guard is an authoritarian decision maker that is charged with properly allocating shots. It’s very much a Pigovian solution.
I hope you’d agree that point guard play is even more important in college than in the pros. That’s because college players don’t really understand the game and there is a strong tendency for better players to try to dominate and take too many shots. The point guard has to be aware of the fact that the team’s expected points are maximized by restricting the star’s shots. I think pros are more aware of this than college players and the point guard’s role as shot allocator is always critical, but especially so in college.
I went to UNC in the 1980s and the joke was that Dean Smith was the only one who could hold Michael Jordan to under 20 points a game. Your example makes demonstrates that Smith was indeed a brilliant coach.
Thanks for a nice example.
P.S. The Ewing theory has not been tested. You can’t sit there and cherry pick anecdotes of teams that do better when a superstar goes down. If there’s any truth to this, however, I’d say it’s not Ewing’s fault, but the point guard’s!
Humberto,
Thanks for checking my arguments. Your analogy of “each possession as a car” is exactly what led me to come up with this idea!
This is probably more directly illustrated with a football example. Specifically, why lousy rushing teams even bother to try and run the ball, rather than just throw all the time. The most often stated answer is that the mere act of rushing keeps the defense balanced and improves the team’s ability to pass, thus improving the offense as a system, despite the negative odds on any rushing play. I’d love to see your analysis of that argument, especially an exploration of the limits of the logic, such as how far the college Spread offenses have bent this rule, and whether or not the West Coast offense can truly replace the run game with short passes. Thanks!
The phenomenon looks like what Dean Oliver (stats analyst for the Denver Nuggets) called “skill curves” in his book “Basketball on paper”.
The curves are actually very hard to find, because basically you are looking for inefficiencies and of course coaches/players are trying very consciously to avoid them.
It should be noted that skill curves are highly individual and the importance of the defensive aspect: not only each player has a different personal optimum, their defensive skills aren’t equal either.
So, the individual personal optimum is not always the best choice, it depends on team makeup. If your team has four guys whose personal optimum is a 16% usage rate but are great defenders/rebounders, a player who can have an iversonesque usage rate of 35% at a tolerable lower efficiency, can be a good idea (see Sixers, 2001).
Your thread has been noted here
http://sonicscentral.com/apbrmetrics/viewtopic.php?p=27313#27313
If you or others here like to discuss this or other applications of analytics known by physicists to basketball feel free to join in. I’d welcome more related to networks, chaos and waves and whatever else.
Everyone,
If you’re really interested in the topic, I highly recommend following the link above from Crow. These guys are professionals, and APBR Metrics is far and away the best forum for discussion of basketball analytics.
I attempted to to create a spreadsheet that would approximate your graphs. My best guess is that Patrick will shoot 80% on his first shot and each additional shot will be 2.8% less likely to go in than the last. If you assume the team will take exactly 100 shots you can plot the amount of points the team will score against how many shots Patrick Ewing takes. If Patrick takes 0 shots the team will score 90 points. At 10 shots the team will score 95.13 points. At 20 shots the team scores 96.76. The team maxes out at 21 shots for Patrick, scoring 96.77 points. Unfortunately, Michael Jordan will shoot 23 times and the Bulls will win 99.52 to 96.77 🙂
The key point here is that Patrick should be allowed to shoot such that his last shot had a greater than a 45% chance to go in and his next shot will have a less than 45% chance to go in.
If Patrick shot to the point where he shot 45% the team would score a measly 90 points and his last shot would have a less than 23% chance of going in. I think I was at that game…
But NBA teams aren’t trying to maximize their field goal percentage, they’re trying to maximize their total score (offensively at least), much like a firm isn’t trying to maximize average total revenue (or minimize average total cost) of its product; it’s trying to maximize profits. To maximize score or profits you always need to equate your margins, and Ewing should shoot up till the point where the marginal benefit of him shooting is equal to the marginal cost, which is, in this example, is exactly the point where he reaches 45%. This example doesn’t explain the Ewing paradox. I think you could still show this, but it would need to be similar to the traffic example, whereby there are at least two steps in the decision making process and the presence of Ewing acts as “the free road” that leads to inferior outcomes… wish I had time to work on this, but I’ll leave it up to others for now…
I don’t think I agree. In what way is “total field goal percentage” not equivalent to “total score”? I don’t see a difference without bringing in something like “decline in defensive effectiveness as offensive output is increased.”
First off, I like the idea of the article. I’m a math teacher and a basketball coach, so I find much to consider here!
Field goal percentage isn’t equivalent to total score for many reasons. One is offensive rebounding (which is probably somewhat significant). Another is dealing with fouls (which I think is significant). When shots are taken close to the basket (by a guy like Patrick Ewing), there is a much higher chance of drawing a foul. Note the two benefits of this play – getting the chance to score and perhaps removing one of the opponents better players if they get in foul trouble. Another yet would be the ability of a player to take advantage of the defensive focus. Some guys will still try and shoot through a double (or triple) team, while others learn to find the open man.
Good point. Mike G at the APBRmetrics board suggested the simple upgrade from “field goal percentage” to “true shooting percentage”, which takes into account free-throw rate and would probably make the argument a bit more sound. http://sonicscentral.com/apbrmetrics/viewtopic.php?p=27313#27313
Here is a sample of a more trusthworthy analysis, where skill curves are defined in terms of TS% and not just regular FG%:
With the 3 point shot maximizing total field goal percentage may not maximize score. You can shoot a lower 3 point % and still score more points.
True shooting percentage is intended to account for this. The exact formula varies, but is usually something alone the lines of
TSP = points / (2 × FGA + k × FTA)
where k represents the long-term proportion of FTA that are the result of a shooting foul on a non-made basket (or something like that). Ideally, you’d just like to know the total number of shots attempted, including those on shooting fouls, but that statistic is not typically available, so this proxy is used instead. A typical value used for k is about 0.88. Note that it is possible to achieve a TSP greater than 100 percent.
Cf. effective shooting percentage, which is usually defined as
ESP = (2 × two_point_makes + 3 × three_point_makes) / FGA
Relative to TSP, ESP penalizes those players that are especially effective at drawing shooting fouls.
Overall, the team is trying to maximize points per possession (PPP). The interesting question is: When the team is maximizing the PPP, what is the usage rate and TSP of the superstar, as opposed to his teammates? In practical terms, how aggressively should the superstar be looking to score, as opposed to passing the ball?
Oops, the denominator on ESP should read 2 × FGA.
nice article, but, maybe, there’s a flaw.
you over-simplified the game, assuming that it’s all about scoring: wages of wins guys would not agree 🙂
p.s.: is it possible to have correlation coefficient value for the graphs? do you have LBJ data?
There is obviously no account for defense here… which is notoriously difficult to quantify. I’m not trying to replace John Hollinger or David Berri any time soon.
With reference to the Ewing example, it must be clear that a simple look at the stats confirms that Ewing definitely should had taken less shots that particular year (the 98/99 season).
Ewing had a remarkably low True Shooting %, lower than any regular rotation player, in fact. And his Offensive Rating (a measure of individual offensive efficiency) was low too, as low as guys like Kurt Thomas or Charlie Ward (none of which was known for his offensive skills).
And still, Ewing was using 28.4% of his team possesions (down a bit from the past year, but still too high).
Indeed, the playoff sucess of that team can be understood by noting how, in the playoffs, Ewing’s usage rate drops from 28% to 22%, with the bulk of that possesions going to Sprewell. Just like that, a really poor offensive team (26 in the league that year) becomes an adequate one, and reaches the Finals.
The “Nash” terminology is confusing here; there’s nothing that looks like a Nash equilibrium to me in the suboptimized policy. But the idea is right given the assumptions.
My only problem with this analysis is that the player knows how much defense he faces BEFORE he decides to shoot, so simply counting shot totals is throwing away critical information. How about if Patrick only shoots when he has a better than 45% chance of scoring and passes it off otherwise? Then all will be well. I’m told some basketball coaches try to teach this with “red light,” “yellow light,” and “green light ” rules for different players shooting in different situations.
I may well be using the terminology wrong. My training in economics is essentially nil.
I bet that real coaches use some considerations similar to the ones I’m talking about here. I’m sure they know that not all of their scoring options are equivalently effective, and they probably make an effort to maintain a kind of artificially even distribution of shot selection. So in a sense nothing in the post is groundbreakingly new. But I think it might do us analytical types a lot of good to formalize the reasoning.
I like the read! The idea that a franchise player could become less than that due to being “too good” is hard to imagine at first, but it makes sense now that I really think about it. But I think something else that’s part of the problem is Patrick Ewing’s decline that factored into the Knicks playing well despite being out for the rest of the playoffs. Ewing had been battling an Achilles Tendon injury since the regular season (if memory serves correctly it was the lockout-shortened one), and played in only 38 of the 50 games of the lockout shortened season that year. I think the fact that the team had to adapt to playing without Ewing, resulting in their second and third options being force to step up improve their scoring efficiency, may also have contributed to that effect. Nevertheless, a great read about how increased use of a star player may actually dampen his effect on the game..
I’m not sure my critique of the applicability of the analysis was clear enough. That’s what I get for writing more like a sports fan and less like a pedant. Warning: pedantry ahead.
The assumption in the original post is that a team commits to a shot distribution in advance of confronting the defense. In dynamic game theory this is sometimes called an “open loop” equilibrium concept. But the real game has “closed loop” strategies–the offense gets to select its shooter AFTER it sees the commitment of the defense against its various options on each trip down the floor. This has two important consequences:
1. The empirical skill curves are not exogenous efficiency schedules but rather endogenous equilibrium results of the teams reacting to the defensive deployments they see. Counterfactuals about what they “would have” scored with different shot distributions cannot be read off these schedules because if they changed their shot distributions the defenses and the schedules would change too. This is a classic endogeneity problem familiar to empirical economists.
2. From an applied theory point of view it is not clear what the meaning of an exogenous skill curve in basketball would be, or rather, what is the x axis of such a curve. As mentioned above, the information set of the players includes where they are on the floor, where their teammates are, where the defense is, etc. A strategy in game theory is a mapping from information sets to permitted actions. The x axis of these skill curves thus does not correspond to a set of alternative strategies; in fact, there might be multiple strategies (even an infinity) that generated these shot distributions.
3. If we imagine a smart team that always took the best available shot on each possession, that might indeed yield the “optimal” distributions as analyzed here, but it would of course depend on the way the defense chose to play and how the team was functioning on that day and so would come out only by chance. Games where Kevin Garnett takes a ton of shots might be games where Ray Allen is getting ball denied and Paul Pierce is in foul trouble so that having him force up some tougher shots on the margin makes sense. In other words, conditional on the game conditions, Garnett taking “too many” shots might be optimal. (I say that as a Celtics hater who always had a lot of respect for KG as a great team player). I remember Wes Unseld, when he was the 6’7″ center on a Washington Bullets team that had scorers like Elvin Hayes and Phil Chenier, that if he scored 20 points it meant that the team was in trouble.
I know that bball is not your normal forte but you have to check out the Wages of Wins Journal(dberri.wordpress.com). He’s found the basis of this article to be false.
The Wages of Wins hasn’t addressed this problem directly, so I’m guessing what you mean is something like this:
It has been shown that equating “a player’s field goal percentage” with “a player’s contribution toward winning” is a mistake, and that’s what this analysis seems to do. If that is your statement, then I agree with you; in general you need something more sophisticated that takes into account defense, rebounding, and free throws generated.
The purpose of a this article, though, was to be a “plausibility argument” and not a proof. Its main conclusions turn only on the general idea that a player becomes less effective offensively the more he is used. If this is the case, then something like Braess’s paradox in basketball is possible. A team that looks for the highest percentage option each time down the court will not do as well as a team that employs a strategy optimized for the entire game. Losing a good player can, possibly, have the surprising consequence of pushing a team closer to the optimized strategy.
Does it happen very much? I don’t know. I didn’t mean to claim that it does, or that every team would be better without its best player (which would be ridiculous). I only meant that we should look into it.
No, he’s shown that the claim that FG% decreases with # of FG Attempts is false.
That’s a very delicate issue, but I have to believe it’s true at some level. Surely any player would do worse if he tried to take every single shot than if he only shot on rare occasion. Please see our discussion at the APBRmetrics forum on if/how the dependence can be born out from shooting data.
Hi there. A couple of thoughts. I haven’t had time to read through all the comments, so if these points have been made, apologies. (Looks like srp made some of these points, but let me ramble on all the same.)
First of all, diminishing returns: This is an expected consequence of rational shot choice. The rationale is simple–presumably, you always shoot higher-percentage shots; it’s the lower-percentage shots that you might think about. If you shoot all shots (and only those shots) which you have a 60 percent chance or better of making, your shooting percentage is going to be higher than if you shoot all shots (and only those shots) which you have a 40 percent chance or better of making.
However, which shots have a better chance of going in depends on the defense, and this goes into my second point: Your analysis treats the impact of defense indirectly (through percentage of shots taken). From a game theoretical perspective, it’s incomplete. So the point at which your Ewing curve crosses the 45-percent line is not really a Nash equilibrium, because the defender’s choice of strategies is not directly taken into account.
In particular, if Ewing takes 21 percent of the shots and shoots 60 percent, while his teammates shoot 45 percent, the defense is not being efficient. They should double Ewing more and force him to pass more to his less efficient teammates. They should, as a result, become slightly more efficient (a side effect explicitly assumed trivial in your analysis, OK), so they’ll double Ewing less, etc. The true Nash equilibrium is reached when neither the offense nor the defense can alter their strategy to improve their outcome, as represented by (true) shooting percentage.
A few weeks ago, I looked at more or less this exact situation
http://thenullhypodermic.blogspot.com/2009/06/game-theory-and-wing-block-dynamic.html
except I used Kobe as my superstar player, and also he’s a wing (or perimeter player) rather than a post player. Under certain fairly unremarkable assumptions–for example, that players shoot worse over a double team than they do over a single team–the expected game theory outcome derives: The Nash equilibrium, when both superstar and teammates shoot the same percentage, is the best either side can expect to do. The offensive team cannot do better by backing off on their superstar player, because the defense will sag off. He will shoot better, but his teammates will shoot worse, and the latter is of greater magnitude than the former at Nash equilibrium. I didn’t show the analysis in my post, but it’s not difficult.
All that being said, there is an important difference between starting your offense at the wing as opposed to the post, which I also mention in my post: The possession does not end at the shot. There is also the rebound. Normally, the defense has the advantage on the rebound. This doesn’t change much when the post shoots over a double team, since the defense is then packed in around the basket. (It does argue for post moves toward the baseline, rather than toward the middle, though.)
However, when a wing player like Kobe shoots over the double team, he draws his defenders away from the basket, and the offense–though it likely never gains a true advantage–is at less of a disadvantage than usual. Perhaps it gets 15 percent more of the rebounds than usual, and those rebounds lead to high-percentage shots. This means that at a truly optimal strategic choice, the wing should increase his shot-taking until his shooting percentage drops BELOW that of the post, by a margin equal to the increase in shooting percentage from offensive rebounds. Because Ewing played mostly from the post, this wasn’t an effect that he could take as much advantage of. Some, perhaps (weak side rebounds, anybody?), but not as much.
What would be interesting would be to find the conditions under which a true Nash equilibrium was not the globally optimal for the offense; that would be a real case of an analogue of Braess’s Paradox. My guess is that this would require something like a non-monotonic shooting efficiency for some player as a function of defensive intensity on that player.
Wow, that’s quite a post. A similar approach from a different angle; I wish I had come across it before I wrote this one.
If I understand your main objection (and srp’s) to my approach, it is that I am treating each player’s “skill curve” as a static relation that the defense cannot change. In essence, I am reducing basketball to a one-player game (or one team of players). In reality, though, a defense should have the freedom to change their focus in such a way that the skill curve of a given player is shifted up or down. So, my claim that this hypothetical team will perform best when Patrick takes 21% of the team’s shots may not be correct. I have forgotten that the defense is also a “player” in this game, and can lower Patrick’s shooting percentage, even if his offensive load doesn’t change.
This argument seems to me completely correct in principle. And maybe it destroys the effect I am claiming (that a team’s best possible game is not one where every player shoots the same percentage). But I can’t see a way of evaluating how important it is. If a skill curve is a notoriously difficult thing to extract from data, the extent to which such a curve can be a dynamic product of the defense seems almost impossible to quantify.
Am I correct in my interpretation of your point? And do you see a way that your arguments could be tested empirically?
You’ve stated my point correctly. As to whether it could be tested empirically, I think it could, in principle, but I think it would require either (a) direct observation of a lot of games, or (b) better statistics than are currently available. (To the general public, at least: I understand that a few teams employ statisticians who watch video and “tag” plays to allow a finer granularity in analysis.)
One could do a proxy analysis by looking at the correlation between, say, Kobe’s shooting rate, his true shooting percentage, and his team’s points per (major) possession. This works to the extent that what Kobe does sets up shots for his teammates, which happens a lot, but not nearly all of the time. For instance, other players do set up shots for themselves or their teammates; Fisher is (in)famous for the PUJIT (pull-up jumper in transition), which many of us Lakers fans would prefer he shoot fewer of, frankly. But it might be sufficient to detect the effect, although quantifying it would be fraught with peril.
If the teams were always rational, then the analysis would generally hold, and the Nash equilibrium would be optimal for both sides (modulo rebounding and the like). However, teams are not always rational. This is the part I deleted from my post, incidentally. I believe that team tactics exhibit hysteresis, and if Kobe comes out bombing right from the start and then later backs off (or vice versa), the defense will take some time before it responds to that change. One can take advantage of that. I also think that Kobe can shoot just a little more than at the Nash equilibrium, thereby drawing more double teams than he really merits (though he does merit quite a few), and finding a better operating point than at the Nash equilibrium. And so on.
In the end, though, I think it’s basically a bar argument for nerds. Very difficult to settle (at least with today’s technology) and therefore rife with potential for speculation.
We have quite a few interests in common, by the way; one of my upcoming posts will be a look at rubbernecking on the highway.
No addressing the fact that Garnett’s fit is only 17% once TS% is used?
nice!
I’ve gotten my bachelors in physics and I’ve been playing ball since puberty. I’ve only applied the basic laws of physics (gravity, forces, angle ..etc) to the game, but I’ve never applied stat anal to the play calling (brasse and ewing), it’s something to think about the next time dude at the gym is taking 1000 shots or when I freeze out a teammate who doesn’t shoot high quality shots…
I think your math is fuzzy. To assume a star’s average teammates can sustain or even perform at a certain level without the star in there is a joke.
I love the geekiness of this article. I love it so much that I want to join in on the fun. Assuming that your observations/theories are correct about directing “the traffic of the game” between the players on the team, how then does this impact the individual play of the players. Once it’s decided that Patrick will take the shot for the team. What type of shot should Patrick take? Shouldn’t he also try to vary the type of shot he takes in order to keep the defence of balance, and thus sometimes choose to attempt lower percentage shots? And here, lies a problem that might help explain the Ewing theory a little further. Maybe I’m wrong, but I don’t remember Ewing have a great variety of shots in his arsenal. Over the course of a game, a good defender will be able to pick up on the timing and rhythm of a move/shot the more he sees it. So those shots will become harder for Ewing to make because they will be better defended as the defender gets versed in Ewing’s moves, even without a double team. Unlike Ewing, Hakeem had a crazy arsenal of shots and moves. A defender, even over the course of a game, would find it nearly impossible to predict what move was coming next, because Hakeem had all the moves, in very much the same way as McHale. There is no Hakeem Theory because of this reason. And there is no Kareem Theory for a totally different reason. Kareem perfected an almost unguardable shot and went to it over and over and over again – the SkyHook.