When Nature plays Skee-ball: the meaning of free energy

The goal of physics is to predict the future.  Usually, practitioners of physics limit themselves to addressing only the most simple and precisely-stated questions, like “if I throw a ball upward, how long will it take to come back down?”, or “if I apply 10 volts across a piece of metal, how much current will I get?”  Occasionally, however, we develop general rules of thumb for predicting the future, which we apply liberally when we can’t fully grasp all the details of what is happening.  Much like psychics or astrologers who follow general rules like “a person born under the sign of Ares will tend to be passionate and energetic” or “a dream of losing your teeth suggests a weak-willed and apathetic personality”, physicists adhere to the general rules of “a system tends to settle into its lowest energy state” and “a system tends to settle into a state of maximum entropy.”  But what if a person born under the sign of Ares has a dream of losing his teeth?  What if the state of lowest energy is different from the state of maximum entropy?

Unlike astrology or psychic readery, physics is required to be perfectly consistent with itself.  So while the first of those two questions may not have a satisfactory answer, the second must have a precise solution.  If it didn’t, you could feel free to dismiss physics as a load of mystical quackery.  So of course there is a way of reconciling the two “rules of thumb”, and it comes by introducing a “modified energy” which is a particular combination of energy and entropy.  We call it the “free energy” (where E is the energy, S is the entropy, and T is the temperature), and our new dogma becomes “a system tends to settle into its lowest free energy state.”  But what’s so magical about this particular combination of energy and entropy?  In this post, I’ll explain where free energy comes from by imagining what would happen if Nature played a game of Skee-ball.

A fair game of Skee-ball

Imagine you’re playing a slightly modified version of Skee-ball, with point values ranging from zero (the gutter) to 40 (the top).  It’s also a somewhat easier variation of Skee-ball, where each of the five possible values are equally easy to roll (the bins don’t get smaller for higher point totals).  I imagine it something like this:

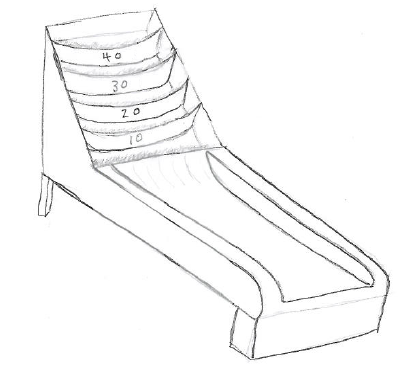
A simplified (and easier) version of Skee-ball

Assume that you’re not very good at Skee-ball, so you’re equally likely to roll a 0, 10, 20, 30, or 40.  The game gives you 10 balls, so what should you expect to get as a final score?  If you’ve read the post on entropy (and if you haven’t, please do) you already know the answer: you should bet on rolling 20 * 10 = 200 (that’s the average of your possible rolls times the number of balls you get).  That’s because there are many more ways to roll something close to 200 than anything else.  To be precise, there are 856,945 distinct games that lead to the total 200, so it’s a pretty good bet.  The number of combinations for each outcome is shown below; you can tell that 200 is the “maximum entropy score.”

This would be the end of our analysis, and we would be ready to conclude that your most likely score is 200, the state of maximum entropy…  except for one thing.  What if rolling a 40 is harder than rolling a 10 (as in real Skee-ball)?  So far in this post and in the entropy post, every game has been played with “fair dice”, where all possible outcomes of a single trial are equally likely.  But what if the dice are weighted, so that higher numbers are harder to come by?  This situation is not only possible in real life, but almost certain to be the case, as we shall see when Nature tries to play the game.

When Nature plays Skee-ball

Imagine now that our modified Skee-ball game is being played by your 4-year-old cousin, whom I will call Nature to be cute (and I will also assume that your cousin is a girl, since the real Nature always gets personified as a female).  Nature isn’t strong enough to consistently roll the ball to the higher numbers, so for her a given roll has a higher likelihood of being a 0 or 10 than a 30 or 40.  We can guess that the probability of her rolling a particular number decreases exponentially with the amount of energy required for her to get the ball up to that height.  Assuming Nature is generally strong enough to get the ball up to the 20 without too much effort, the probability distribution for a single roll might look something like this:

The probability that Nature rolls a particular value decreases exponentially with the amount of energy required to get the ball that high. The dotted line is a "fair game", where every value is equally likely.

So how does this distribution affect Nature’s most likely final score?  There are still 856,945 ways for her to roll a 200.  But is 200 still the most likely score, now that rolling a 20, 30, or 40 is less likely than it used to be?  The answer is no: her most likely total is going to shift downward, like this:

When Nature plays Skee-ball, her most likely score is lower than yours.

You can see that 100 is Nature’s most likely score.  But what’s special about 100?  It’s not the score with the maximum entropy (that would be 200), and it’s not the score with the minimum required energy (that would be zero), but it is the score that has the highest probability of occuring.  So it must be the score with the smallest free energy.

What Ludwig Boltzmann had to say about this

When I assumed earlier that the probability of a particular outcome decreased exponentially with the amount of energy required of Nature to produce it, I was in fact hinting at a very fundamental truth.  This is the law of the Boltzmann distribution, which says that the probability of a given outcome is directly proportional to .  The quantity is called the “thermal energy”, and it is best thought of as the amount of energy that can be readily given to an object by the surrounding environment.  An event requiring a very large energy E is unlikely to happen spontaneously, whereas an event requiring can easily happen on its own.

Just to make this idea concrete, imagine a single air molecule near the surface of the Earth, bouncing around randomly through the atmosphere.  You can ask: over what range of altitudes is this air molecule likely to travel?  Well, for the molecule to be very high above the surface of the Earth, it must somehow acquire enough energy to beat the gravitational force and arrive at that height.  The molecule can get some energy by randomly colliding with the air molecules around it, and the amount that is readily available is (about Joules at room temperature).  This suggests that the air molecule can only go high enough that its gravitational energy is equal to .  Going higher is possible, but exponentially rare: it requires a number of highly-energetic collsions with other air molecules.  This is why the density of Earth’s atmosphere decreases exponentially with altitude.

So there are two things to consider when trying to figure out what outcomes are most likely: the number of different ways you can arrive at that outcome (the entropy), and the energy cost associated with the outcome.  The total probability P associated with some outcome is proportional to the product of the two considerations: , where is the number of distinct configurations that lead to the outcome and E is its energy.  The most likely state is the one where is maximized.  Take the logarithm, and you’ll see that maximizing is the same thing as minimizing the quantity .  Compare with the definition of entropy, and you’ll see that we have arrived at the free energy: .

So what’s so special about free energy?  It is the combination of energy and entropy that balances the effects of probability decreasing with energy and probability increasing with the number of possible combinations.  Saying “a system settles into its state of minimum free energy” is just a way of saying “a system assumes its state of maximum probability.”  But now we have a more accurate way of predicting what that state will look like.

If the temperature (amount of thermal energy readily available) is large, then look for the state with maximum entropy (the most “disordered-looking” one).  This is like when you played Skee-ball: having enough energy to roll a 40 wasn’t a problem, so the most likely outcome was the one with the greatest number of ways to arrive at it.

If the temperature is small, then look for the state with minimum energy.  This would be like an infant playing Skee-ball: they can can hardly provide enough energy to roll the ball at all, so expect them to roll a zero (the lowest energy total).  At zero temperature, you would also expect the air in the atmosphere to collapse to the surface of the earth.  Each air molecule would assume its state of lowest energy.

And of course, for anything in between, you must balance energy and entropy by talking about the free energy .  In case you’re curious, the free energy of a given total for Nature’s Skee-ball games looks like this:

You can see the free energy minimum at a score of 100, the most likely outcome.  The same way we think that a ball rolling around in a gravitational potential well will eventually come to rest at the bottom, we tend to think that a system moving around in its “free energy well” will eventually come to rest at the minimum.  That’s one of the main benefits of defining free energy: it helps us use our beloved “ball rolling around at the bottom of a hill” analogy.

And of course, if you were to play a very long game of Skee-ball (say 1,000,000 balls instead of 10) the free energy minimum would become very sharp, meaning the probability of getting the “minimum free energy score” would be overwhelming.  Near the end of the entropy post I said “thermodynamics is like a game played with dice”.  Well, I guess it’s also a lot like a game of Skee-ball played with balls.