The Universe is a giant energy minimization machine
Physics, at its worst, can be tremendously complicated. Sometimes learning physics (or any other branch of science) can seem having to memorize a giant catalogue of phenomena, each discovered by some guy who got an equation named after him. It can seem like if I want to solve a problem, then I need to begin by preparing a huge cheat sheet of possible relations and dependencies that have to be taken into account. For example, if I were solving a problem in atmospheric physics, I might feel compelled to make a list like this:
- Remember that charged particles drift in crossed electric and magnetic fields (…formula…)
- Remember the coriolis acceleration (…formula…)
- Remember relativistic effects (…formula…)
- Remember that ionization depends exponentially on temperature (…formula…)
- etc.
Apparently, solving a problem in atmospheric physics requires me to remember and understand all these effects, plus dozens of others, and decide how each will affect the problem. What an ugly mess! I would never have chosen to become a scientist if I knew it would be like that. And sometimes, for sure, it is. I have definitely read some ugly scientific papers, in which a bunch of different effects (each with its own formula) get patched together to form some awful and unintelligible Frankenstein theory.
That’s not to say that all the different effects in physics aren’t interesting. They usually are, and discovering a new phenomenon is the rush that everyone studies physics for. But no one wants to approach every problem by making a long list of things they have to remember and then making sure that each one gets its say in the answer.
Luckily, physics doesn’t actually have to be like this. Strangely enough, I find that the more I study physics and expand my “catalogue of effects”, the more I end up approaching every problem the exact same way. That is, instead of adhering to a big messy list, I am guided by a single principle:
- Remember that the universe is a giant energy minimization machine
I’ve talked before about how energy is the most important concept in physics. But I’ve realized lately that the degree to which I rely on it for solving problems is kind of astonishing. In fact, these days I approach just about every problem using the same three steps:
- Draw a big picture and write out all the things that can possibly happen (usually by defining some mathematical variables).
- Decide how much energy the various possibilities require (usually by writing down some equations).
- Find out which possibility has the lowest energy (usually by minimizing those equations). This is what will actually happen.
Now, these steps can be deceptively hard, but the approach is remarkably simple. If you want to know what will happen to some object or set of objects in the future, you just have to remember this: of all the options available, the universe will choose the one with the lowest (free) energy. It may be hard to describe how that thing will happen, but you can rest assured that eventually it will.
In this post and the next one, I want to give an example or two of surprising realizations you can reach by adhering to the doctrine that the universe will somehow find a way to minimize its total energy.
Example #1: a mysterious force of suction
Imagine performing the following experiment: you take two flat plates of material and give them equal and opposite electric charges (if you want, you can do it the way they did it in the 1600s: by rubbing a piece of glass against a piece of resin). Once you’ve done that, take your plates to a big reservoir of water, and hold them parallel to each other so that their bottom edges just barely touch the surface. Like so:
The lines here indicate the presence of electric field: since there are positive charges next to negative charges, there is an electric field going from positive to negative. If the plates are fairly large relative to the area between them, then the electric field lines will be pretty much parallel and horizontal.
This is the end of the experimental setup. What will happen?
At first, it looks like nothing should happen at all. The plates attract each other, but you are holding them in place so that they can’t move. The only other possibility is that maybe the water could be pushed around by the electric field. But it doesn’t seem like this should happen either, since the electric field goes in straight lines and apparently doesn’t even touch the water.
But try approaching this from the perspective I advocated in the introduction. Don’t ask “what forces are pushing things around?”. Instead, ask “how could the universe lower its energy?”. The answer to that question is a little more interesting.
In this case, there is some energy to be saved by bringing water in between the charged plates. That’s because water has a high dielectric constant (about 80 times larger than air), so if there is water in between the plates then the strength of the electric field is diminished. And electric field is a type of energy (with energy density ), so if you reduce its magnitude then you lower the energy of the universe. You can also think of it this way: water molecules are polar objects, with a positive end and a negative end. Each of them would gain some energy by being in the presence of en electric field, where they can point their positive ends toward the negative charge and their negative ends toward the positive charge.
Apparently, then, there is some energy to be gained if the water spontaneously jumps up in between the two plates. And, in fact, it does, like this:
 This is a conclusion that we might not have reached from the beginning. There don’t seem to be any strong forces pushing the water upward. But the water gets sucked up nonetheless, because the energy of the universe can be lowered when it does.
This is a conclusion that we might not have reached from the beginning. There don’t seem to be any strong forces pushing the water upward. But the water gets sucked up nonetheless, because the energy of the universe can be lowered when it does.
If you want to figure out how high the water level rises in between the plates, then you have to balance this electrostatic energy savings with the cost of picking up all that water against the earth’s gravity. You can do so by writing down the total energy as a function of the water height and then finding out which value of
minimizes the total energy. For anyone following along at home, I’ll give the final answer [UPDATED]:
.
Here, is the charge on the plates,
is their area,
is the vacuum permitivity,
is the acceleration due to gravity, and
is the density of water.
You may find this answer pretty unsatisfying; certainly I did when I first encountered it. There seems to be a contradiction: at the beginning of the problem there is no force acting on the water molecules, but somehow they rise up to fill the space between the plates. How is that possible?
The answer is that there is, in fact, a force on the water molecules. My description above of the electric field — that it goes in straight lines and exists only between the two plates — isn’t really correct. The electric field bends a little bit at the edges and at the boundary of the water surface. This bending is enough to provide a force that pushes the water upward and holds it there once it has risen. This a subtle point. But, amazingly, we didn’t need to know it in order to figure out what would happen (or even to calculate the magnitude of the force). Just knowing the general behavior of the electric field, and how much energy it stored, was enough to figure everything out.
For those of my readers with a background/inclination toward economics, I pose the following question: do you think about economics problems in a similar way? Do you approach them with a similar guiding principle, like “a person or population will do whatever results in the maximum income?”, even when it’s not clear how or why they should do that thing?
When I taught introductory physics, I liked to state the parallels between energy and money explicitly: it isn’t created or destroyed, and everyone is trying to get as much (or for energy, as little) of it as possible.

As an economist I like the idea of finding an analogous ‘law of energy minimization’. My tuppence worth for discussion:
‘Money flows to scarcity’
or
‘All invisible costs want to become visible’
or
‘The optimum choice minimises opportunity cost’
… thanks for the inspiration!
Energy is for statics. The universe is dynamic, and seeks to extremize action!
I really do need to write a post about the least action principle. It ties in closely to all my talk about “the quantum field”.
But I have to admit that I still struggle with it a little bit from a philosophical standpoint.
This is interesting. Yes, economists tend to think of competitive markets as automatically accomplishing the efficient outcome (generating the most total good)…but there are caveats and caveats and caveats. Would you say that physics is free of these, or just free enough that the energy minimization principle is usually a pretty good guide?
We could compare the ways markets fail to their analogs in the physical world. For one, I suppose the universe doesn’t need to worry about whether property rights are well-defined, and other human constructs. Perfect information isn’t a problem in the universe either; gravity just acts between two bodies, unconditionally. Another way markets can fail is if there are too few agents (e.g. monopoly is inefficient). Do you ever run into issues in physical situations where there aren’t so many zillions of molecules bouncing around? Maybe you can confirm or correct my physics speculations above.
It seems that physicists are in pretty good shape. But it occurs to me that there’s one really fortunate area we’ve got you beat. If it costs a company $100 up front to make a product it can turn around and sell for $1,000, you can bet it’s going to do it. But because physical objects are not forward-looking, they can’t get over the activation energy hump by themselves. The reason it’s fortunate is that it’s _good_ for society when the firm creates $900 of surplus, whereas on reflection, a universe that truly minimized energy in this way would have…shall we say…some problems.
There are a lot of good talking points here.
First, I should probably say that in practice the law of decrease in energy is primarily a statistical one. When there is no thermal energy (zero temperature), it is strictly obeyed. But at finite energy, it is only true because of the law of large numbers, because the average energy of a zillion interacting particles becomes very sharply defined. In the study of a small number of particles moving around, the behavior has to be described in a less deterministic, and more probabilistic, way.
Your second point, about humans being forward-looking, is also a pretty interesting one. I would say that quantum mechanics does in fact allow for particles to be “forward-looking”. That is, a particle trapped in a potential well can borrow energy from the environment in which it sits in order to jump over any barriers and achieve a lower energy. In fact, philosophically, quantum mechanics predicts that every such barrier will eventually be overcome. But the rate at which a particle can jump (tunnel) through the barrier depends exponentially on how much energy it has to borrow from the universe in order to do so. What’s more, all the energy it borrows must be returned.
Out of curiosity, has anyone ever noticed a similar relationship in economics? If a person can only make money by first borrowing some large sum, does the rate at which they succeed decay exponentially with the amount they are required to borrow?
That’s interesting about the quantum borrowing. I don’t know that exponential decay makes a lot of sense in the general context of success rates when borrowing money etc., but I wouldn’t be surprised if it showed up in some particular, related context.
Speaking of zillions of molecules, here’s an excerpt from the preface of an old textbook by Donald McCloskey:
“The governing image of ersatz price theory is that of one person cheating another, taking ‘unfair’ advantage; that of real price theory is of many people trying to cheat all the others, but in fact helping them. The unintended consequence of selfish behavior is altruistic; the apparent chaos of competition, unplanned by moral or civil law, leads to orderly social change; direct attempts to help this or that person are thwarted by the logic of economic events. Such are the paradoxes in which economists delight. The key to the paradoxes is that each person’s behavior is constrained by all others’ behavior. The person is a molecule in a social gas bumping against other molecules, unable to move in a selfish straight line. The theory of price is based on methodological individualism, adding up the bumping molecules.”
The late Paul Samuelson was express about the influence of minimization principles on his work. I will try to find a quote.
The concept of spontaneous symmetry breaking in far from equilibrium systems has been a guide for me in noticing many macro and micro dynamics that others ignore.
I have on my blog pointed out a few places where post-Feynman work on minimzation in far-from-equilibrium systems might be applied fruitfully in economics. Using the Ising Model to understand how leverage can result in synchronized market-wide buying/selling, for example.
I think minimization principles generalize to social systems. The concept of a general equilibrium in neoclassical economics is predicated on extremization of aggregate utility –a kind of functional.
Wow, that’s interesting. I hadn’t realized that economists had adapted these kinds of ideas from physics to such sophisticated levels.
And if you do find the quote, please post it. I’d be interested to hear.
@Gerard: “Money flows to scarcity”? That seems to contradict the observation that large concentrations of money are used to buy influence over markets which serves to further concentrate money. If anything, money behaves more like gravity than an ideal gas, in that existing inequalities are magnified over time.
@Xan: I think the difference is, as I stated before, physics is dynamic. That is, when everything is stable, you can minimize energy, and ideal markets will reach steady-states in efficient outcomes. But the real work is what happens when the world changes? It’s the process of getting to the steady states that’s interesting, and there are a lot more hooks in human interactions than in physics that prevent the transition from one state to another from proceeding smoothly.
#1 Your perception of markets is wrong then. It’s much cheaper and profitable to “go with the flow” than to try and manipulate entire markets. Successful businesses do not need to manipulate the market, except to satiate demand and increase supply.
#2 Regarding the “dynamic” nature of physics, consider that time is just another variable along with position, and suddenly, nothing is dynamic. Rather dynamic simply means, “Now add in the variable ‘t’ and solve again”. A whole great piece of physics is the study of static “motion” and how it directly applies to dynamic motion.
Also, consider that ultimately, all energy is turned into heat thanks to entropy, and the neat little patterns of motion that particles make soon ends up being a pretty consistent porridge. A very large class of problems are accurately solved by G&L’s method, which is extraordinarily simple and easy to apply in the real world. Use it to understand why your gas mileage diminishes on an upward climb, or diminishes as you drive faster, etc… and you will quickly see its power.
Maybe you can explain what the adage means? Your response sounds nonsensical given the plain reading of the words. I had a feeling that it was jargony, which is why I said “seems”.
As for statics vs. dynamics, that works fine for high school and intro college stuff. Throw in some general relativity, some quantum mechanics, and suddenly you’re talking Cauchy data and time is very different in practice.
But even within basic classical mechanics, when you include time it’s not energy that’s extremized, but action.
Here is the simplest possible example from economics (followed by a few words on more sophisticated examples):
Suppose a world with one lettuce seller and one lettuce buyer. The cost (to the seller) of producing x heads of lettuce is C(x). The value (to the buyer) of x heads of lettuce is V(x).
Given a price p, the seller chooses a quantity x to maximize his profit, which is px-C(x). The buyer choose a quantity x to maximize his surplus, which is V(x)-px. The economy is in equilibrium if the seller wants to sell the amount the buyer wants to buy.
One way to compute the equilibrium is to write down the first order conditions for the seller’s and the buyer’s problems. If x1 and x2 solve those problems, the conditions are: C'(xs)=p for the seller and V'(xd)=p for the buyer.
So to find the equilibrium, we must solve three equations in the three unknowns xs, xd, and p, namely:
1) C'(xs)=p
2) V'(xd)=p
3) xs=xd
But a faster way to find the equilibrium quantities is to pose a different problem: The “planner’s problem” is to maximize social welfare, defined as V(x)-C(x). The value of x that solves this problem is equal to the common value of xs and xd in equilibrium.
This is an extremely simple example (though it already has profound implications about the desirable properties of competitive equilibrium). But in more sophisticated examples, incorporating infinite numbers of goods, goods delivered at different times, decision making in the face of uncertainty, etc., it can be essentially impossible to compute the competitive directly—and in these cases, a common strategy is to formulate an appropriate “planner’s problem”, prove that every competitive equilibrium is a solution to the planner’s problem, and then solve the planner’s problem.
What you’ve done with your water example is nearly perfectly analogous to this standard technique in economics.
Thanks Steven, I like that example a lot, and the paradigm of the “planner’s problem”. I had a feeling that there must be some analogue of “solving by force equilibration” and “solving by energy minimization” in economics, and I’m glad to see that there is.
Sorry I can’t post a full excerpt. See page 21 of Foundations of Economic Analysis by Samuelson
http://books.google.com/books?ei=00xnS8XUHpz2NKS9xJAO&cd=1&id=HeG6AAAAIAAJ&dq=Samuelson+Foundations+of+Economic+Analysis&q=minimization
Although the analogy is not complete, one could call Hal Varian’s nonparametric tests of the Weak Axiom Revealed Preferences in the early ’80s a kind of calculus of variations. Unlike an exact analysis, those tests only establish that WARP is not violated by aggregate data about consumer behavior, making WARP a kind of mean-field approximation to the behavior of individual consumers within the aggregate.
On my view, all the action in economics will be in making perturbative corrections to those mean-field approximations. The behavioralist critique, which goes after the rational hypothesis itself, is built up from a wholly different set of data, and ill-suited to correcting the approximations of neoclassical theory.
Almost all of what I just wrote is speculative and personal. If you find another person who understands both sets of theories (i.e., both field theory and neoclassical economic theory), and they disagree, I’d like to know.
This is a particularly good review article.
http://rsta.royalsocietypublishing.org/content/368/1914/1175
Are you missing a factor of the relative permittivity in your formula for h? It seems that odd that the whole effect is based on the reduction of energy caused by relative permittivity and I don’t see it in your expression. It is this energy gain that must be balanced with the energy loss due to the increased gravitational potential.
Or is that already used in computing the front coefficient 79/160. It could be (e-1)/2e, assuming e = 80.
Yes, that’s right. My 79/160 is actually (e – 1)/2e, where e is the dielectric constant of water. I suppose it would have been easy enough to write that out, but the equation was kind of messy already.
Hi, Nice post and interesting global approach. I’m interested in how to come about the formula for calculating the height that which the water will rise. Could you elaborate a bit on deriving it?
It seems intuitive that the more charge the higher the water would rise, but I find (since d is multiplying) quite counter-intuitive that increasing the separation between the two plates would create a similar effect.
Hi Pau,
Thanks for checking that. You’re right that it doesn’t make sense, and in fact there was a mistake in the formula. I’ve corrected it now, and in fact drops out of the final answer, as you probably expected.
in fact drops out of the final answer, as you probably expected.
The way to derive the expression is to balance the change in electrostatic energy against the gravitational potential energy of the water. The former can be found by integrating the square of the electric field across the volume inside the plates, and I get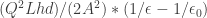 . The latter comes from multiplying the mass of water inside the plates by its average height, which gives
. The latter comes from multiplying the mass of water inside the plates by its average height, which gives  , where
, where  is the width of the plate.
is the width of the plate.
Yes, I approach economics (and by $ proxy all social/political analysis) with the question which maximizes the economy value for the localities involved. As a first rose cut, this usually tells you what is going to happen. Then it just becomes a matter of figuring out how.