When F is not equal to m a: classical examples of effective mass

The world of electrons is a strange place.

It’s not that the actual physical environment in which electrons dwell is so odd; the weird thing about electrons is that they seem to follow a very different set of rules than the every-day objects around us.  This is why physicists and chemists spend so much time obsessing over them.  We have this idea that if we can better understand the strange rules that govern the world of electrons, then maybe we can gain deep insight into the nature of the universe around us.

And, on a more basic level, it’s just fun to stumble around in a strange, alternate reality, discovering it by bits and pieces as you go.  In this sense physicists are like fantasy/science fiction enthusiasts.  We like discovery and we like weirdness.

The weird world of electrons

In this post I want to discuss one of the weirder behaviors of electrons: the effective mass.  Consider, as an example, electrons trapped inside a periodic crystal (a diamond, perhaps).  The world in which these electrons live looks something like this:

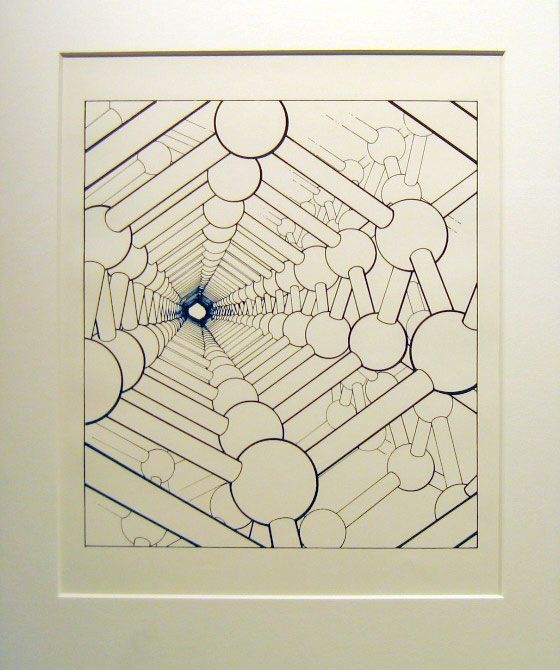
A drawing of a crystal arrangement of atoms, made by Dick Zallen, my first college physics teacher. Click the picture to see more of his drawings.

It’s a dramatic-looking world, but it’s not a terribly hard one to visualize.  You can imagine throwing a ball down one of these crystal “hallways” and watching what it would do: it would bounce around on the atoms, getting reflected in different directions as it went.  You could also imagine a whole bunch of balls bouncing around in the crystal, careening randomly in all different directions.

This is essentially what the inside of a crystal looks like; the “balls” are electrons, careening through the crystal.  The rules that govern the electrons, however, are very different from the ones that dictate the behavior of bouncy balls.  For one thing, the electrons are never allowed to come to a stop.  You can make the crystal as cold and as stationary as you want; even at absolute zero the electrons will still be flying around like crazy (an electron in zero-temperature copper, for example, moves at an average speed of 3 million miles per hour).  This is a consequence of Pauli’s exclusion principle, which says (roughly) that no two electrons can be simultaneously close to each other in space and close to each other in kinetic energy.  In order to follow Pauli’s rule, the densely-packed electrons must keep moving forever, each with a slightly different speed, so that no two nearby electrons have the same kinetic energy.  All this frantic motion is sometimes called “zero point motion” or “zero point energy”.  And no, despite what you see on crackpot youtube videos, there is no way to harness it to turn a tiny object into a source of limitless power.

There is another strange rule that electrons obey.  Namely, it can be surprisingly hard or easy to push an electron around.  That is, the electrons, which have a very well-defined mass kg, will sometimes respond to force as if their mass was ten times larger, or ten times smaller.  On rare occasion you will even find that when you push on an electron it accelerates in the opposite direction.

In condensed matter physics, this strange behavior of electrons gets described by the electron “effective mass”, which can depend on the speed of the electron and on the type of crystal it is sitting in.  We say that the real mass of the electron, , gets replaced by the effective mass .  The kinetic energy, momentum, and acceleration of the electron all behave as if the electron had some mass that can be very different than the real mass .

But why is this allowed?  Doesn’t it contradict Isaac Newton’s most sacred law, ?

The derivation of the electron effective mass that I got in class, which involves Bloch functions and the Schrodinger equation, was never very satisfying to me.  It didn’t really seem to answer my question: why is this allowed?  What I wanted to know was: does there have to be quantum mechanics for there to be effective mass?  Are there any examples of objects in my world (not the electron’s world) which respond to force as if they had some completely different (or even negative!) mass?

As it turns out, there are.  In this post I want to give two examples from classical physics of objects with effective mass that is very different from the real mass.

Before I proceed, though, I want to make the following clear: effective mass has nothing to do with friction.  A lot of times people describe the phenomenon of effective mass as “friction between the electron and the crystal”.  While it’s true that friction can make something feel harder to accelerate, and therefore “feel heavier”, real effective mass cannot be a result of friction.  If it were, than the electron would be hard to speed up but easy to slow down (since friction would help).  Also, the energy that you put into accelerating the electron could not be regained later; it would be lost to heat.  Neither of these is the case with electrons.  Their effective mass does not depend on whether the electron is speeding up or slowing down and it does not imply any kind of energy dissipation.  All the energy that you put into accelerating the electron is retained and can be used later.  It’s just that, in giving that energy to the electron, it responds as if it were significantly heavier or lighter.  How is this possible?

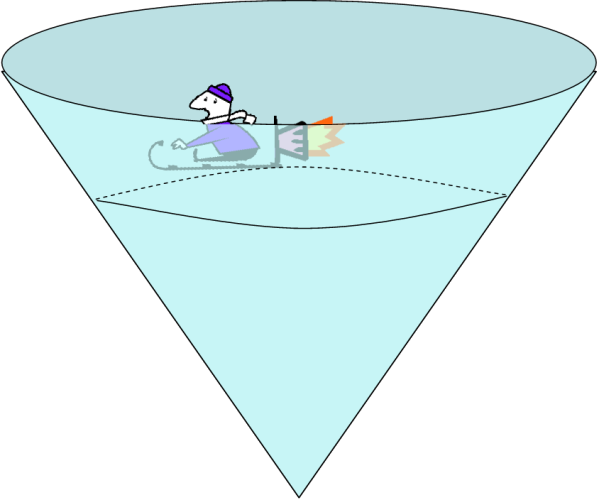
The weird world of rocket-powered sleds

Consider the following situation, which is silly but in a completely non-quantum way.

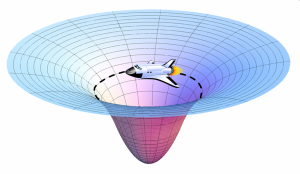
Imagine that you are driving a rocket-powered sled around the inside of a frictionless cone of ice.  Something like this:

 

Because the sled is racing around on a frictionless ring, there is a definite relationship between the sled’s velocity and the radius of curvature on which it is sliding.  For example, if the sled is moving around near the bottom of the cone, then it can be going slowly in that small circular path.   If you speed the sled up greatly, though, it will be going too fast for gravity to hold it in such a small radius (the inward component of the normal force is too small to provide the necessary centripetal force).  So the sled will slide up the side of the cone until its radius of curvature is large enough to accommodate the large velocity.

So there is a definite relation between the sled’s velocity and its height above the bottom of the cone.  You can work it out at home (using some basic force diagrams) if you want, but I’ll give you the answer:

(you’ll find that it doesn’t depend on the angle of the cone).  The total energy of the sled is its kinetic energy plus its potential energy .  Combined, this is

.

The total energy of this sled can be written as , where .  In other words, the effective mass is three times the normal mass.

What does this effective mass imply for you, the rider, as you ride around the cone?  It means that your sled responds as if it were three times heavier than it really is.  When you turn on the rocket booster to speed up, you’ll find that you don’t accelerate according to .  Instead, you accelerate more slowly, like .  The reason for this is fairly simple: it’s not that Newton’s law is violated.  But when you turn on the jet booster, you are paying for both an increase in kinetic energy and an increase in your potential energy as you rise up the side of the cone.  The result is that your rocket sled feels heavier than it would if you were sliding on a flat surface.

That extra potential energy that you paid for, of course, is not lost.  If you turn the rocket booster around and use it to slow yourself down, you’ll find that that the sled is harder to slow down than you expected.  When the rocket fires, the sled velocity decreases, but then as a consequence the sled slides down the side of the cone and regains some of the lost kinetic energy.  So you will feel as if the sled is three times harder to slow down than you would expect; again, the sled feels heavier.

Negative effective mass…  in space!

A spaceship in a gravitational potential well.

One more example: one that is perhaps not as silly as a rocket-powered sled.  Imagine a space ship orbiting the Earth.  The spaceship has some positive kinetic energy, but it also has some negative potential energy due to its gravitational interaction with the Earth.  As it turns out, the potential energy is larger in magnitude than the kinetic energy (if it weren’t, then the spaceship would escape the Earth’s orbit), so the total energy is negative and equal to

,

where is Newton’s gravitational constant, is the spaceship mass, and is the radius of the orbit.  Since the gravitational force holds the spaceship in place in orbit, there is also a relation between the velocity of the spaceship and its radius:

.

Put the two equations together and you get

.

In other words, the spaceship has negative effective mass .

This means that if the spaceship fires its thrusters while it is in orbit, it will slow down.  The spaceship accelerates in the opposite direction of the applied force.

This negative effect mass is a peculiar result of the shape of the gravitational potential.  When you fire the rocket thrusters, your ship is pushed further away from the Earth.  This process consumes both the energy of your burnt fuel and some of the kinetic energy that you formerly had, resulting in a decrease in your speed.  Similarly, if the spaceship fires some reverse thrusters, then it will fall lower into the orbit and speed up.

Again, Newton’s law is not violated when all forces are taken into account.  But for the driver of the spaceship, the shuttle seems to have negative mass.

Epilogue: So what’s really happening with electrons?

So far in this post, I haven’t really explained why electrons are crazy.  I just told you that they are, and then I showed you how classical objects can be crazy too.  I haven’t answered the real question: why do electrons have negative mass?

The short answer is that electrons have effective mass because there is another energy in the game: the electron’s interaction energy with the crystal lattice.  When you change the speed of an electron, you change this potential energy as well, and this makes the electron “feel” as though it were heavier or lighter than it really is (just like the rocket-powered sled or the spaceship).  In essence, the dependence of the potential energy on velocity is the only thing required to give an object effective mass.

For an electron, the reason that the potential energy depends on velocity can be understood with some very schematic quantum mechanical arguments.  Remember that electrons (and all matter) have a particular quantum wavelength called the “de Broglie wavelength”.  That is, an electron is best thought of not as a point but as a wave of negative charge density.  Like this:

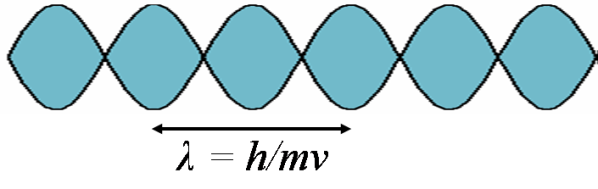The wavelength of the probability wave is related to the speed of the electron: the faster the electron is moving, the smaller the wavelength.  But the wavelength of the electron is very much involved in how strongly the electron interacts with the lattice of positive atoms around it.  Like this:

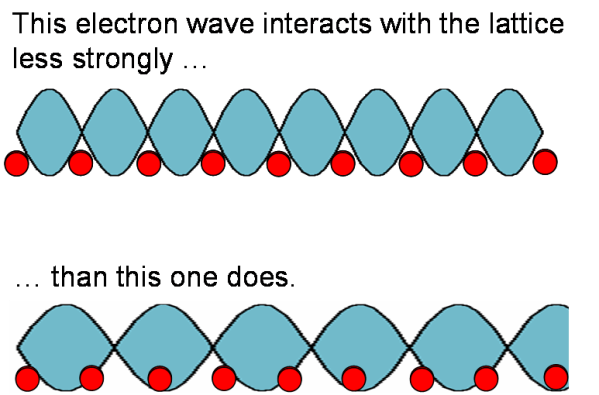
It is this interaction between the (negative) electron wave and the (positive) crystal lattice that gives the electron its strange effective mass.  And crystal lattices can have all sorts of sizes and strange structures, so every crystal has its own electron effective mass: some large, some small, and some negative.

In summary, the world of electrons is indeed a crazy place.  But this particular aspect of its craziness is one that applies to our world as well.