How to trap a particle: quantum wells in 1 and 3 dimensions (Part 1)

One of the more surprising statements in quantum mechanics is that it is impossible to perfectly confine a particle.  This is a consequence of Heisenberg’s uncertainty principle (), which says that the more tightly you try to confine something the more energetic it will become, until eventually it will have enough energy to escape your trap.  I imagine it something like holding a little spring (say, the kind that you can get by taking a clicky pen apart) between your two fingers.  If you don’t squeeze it at all, the spring remains in a low energy state and isn’t going to go anywhere.  But once you start compressing it, it becomes increasingly tense and jittery.  If you get greedy and try to squeeze the spring too much, it will eventually escape your “trap” and sproing away to freedom.  You may well ask what makes a particle “springy” in this way, but the answer is difficult and (to my mind) highly philosophical in nature, and in short is the subject for another day.

In general, a “particle trap” is best described as a “potential well”: a map of how much energy it costs to move the particle to a given position.  Usually we choose the potential energy U to be zero far away from the trap and negative inside the trap, so a characteristic potential well might look like this:

A potential well

This way, a particle with positive total energy is free, where K is the kinetic energy and U is the (negative) potential energy.  Even if it falls into the trap, it has enough kinetic energy to get out again.  Conversely, a particle with negative total energy is trapped — its kinetic energy K is too small to overcome the walls of the trap, which have a height U.  The energy barrier that comprises the “walls” of the potential could be caused by lots of things (electric forces, magnetic forces, gravitational forces, etc.) but we usually talk about potential wells as if something had physically fallen into a hole of some kind.  It aids the imagination, but don’t take it too literally — you can still have a potential well without involving gravity.

If you had never heard of quantum mechanics, you would expect that any well at all would be good enough to trap a particle.  Think of a ping pong ball rolling around on a table.  The slightest divot in the surface of the table is enough to rest the ball in, because a ping pong ball can always have zero kinetic energy (just stop it with your hand and then set it down carefully).  Quantum objects, however, have to deal with the uncertainty principle, which says that the tigher you try to confine them, the more kinetic energy they can have.  And if the thing you are trying to trap has more kinetic energy than the depth of your potential well, it will escape.  So we might expect that quantum mechanics only allows certain kinds of potential wells to trap particles (in physics jargon, we say “only certain potential wells have bound states”).  If the well is too shallow and too narrow, it shouldn’t be possible.  So which kind of potential wells can trap particles, and which can’t?

It is a surprising result of quantum mechanics that the answer depends very greatly on how many dimensions your trap has.  It turns out that it is always possible to trap a particle in a one-dimensional potential well, no matter how shallow or how narrow the well is.  In three dimensions, however, special restrictions apply.  What gives?  When I first learned this result it surprised me, and I tried asking various professors why it should be so.  But mostly I got the party-line explanation of quantum mechanics: the Schrodinger equation says so.  Luckily, I have an advisor who, like me, is not a fan of complicated equations, and after bringing my problem to him he gave me a lovely and surprisingly simple explanation.

Before I go further, I should probably explain what “one-dimensional” and “three-dimensional” traps look like.  In physics, “one-dimensional” doesn’t mean that only one direction exists, just that only one direction matters.  Shown below is an example of a one-dimensional trap: put two very large, flat plates next to each other and trap the particle between them.  Now the particle is trapped in the “x” direction, but is free to move around freely in the “y” and “z” directions.  The y and z position of the particle don’t matter at all to the problem, though, only x does.  So we call the trap “one-dimensional”.  The analogous three-dimensional trap would be a hollow sphere which traps the particle inside.

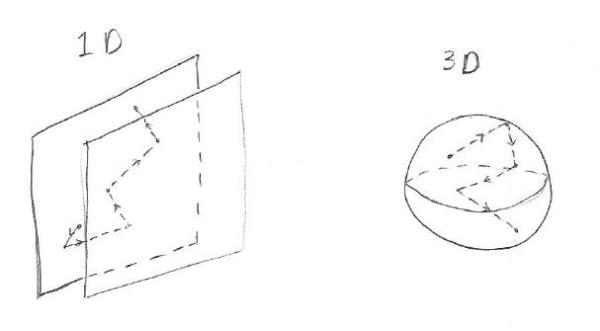
A particle bouncing around inside a 1D and 3D trap

The picture above describes what we call a “square well”: every point on the inside of the trap is equivalent to every other point, and all points outside the trap are also equivalent.  But to get from the inside to the outside the particle has to overcome an energy barrier — it has to break through the wall of the trap.  If you want a weak trap you can imagine the walls being made of tissue paper, while a strong trap might have walls made of steel.  The “material” the trap is made of determines the depth of the potential well.  From now on I’ll do all my reasoning using these kinds of square wells, which have only two characteristics: their depth and their width.  The results we obtain can be applied quite generally, because any potential well, no matter what funny shape it might have, also  has a characteristic depth and width.  Here is a picture of our lovely potential well, which you can imagine in 1D (as the space between two planes) or 2D (inside a long cylinder) or 3D (a sphere):

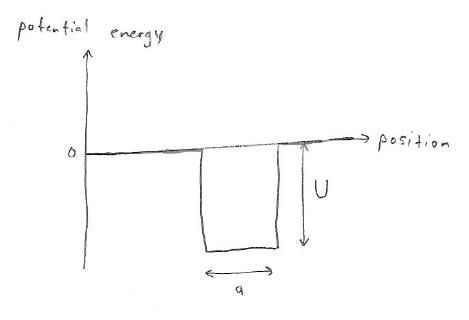
The square well

…this post is getting prohibitively long, so it will have to be continued in Part 2.  For now, at least, we have set up the problem: a particle inside a square well.  But we still have a mystery.  For a 1D trap, the “squeezing energy” is never enough to break the walls of our trap, no matter how weak they are or how close together.  A 3D trap, however, has to obey certain restrictions if it is to contain a particle indefinitely.  Why the difference, and what is the restriction?  The answer is a little surprising, and demonstrates another very peculiar aspect of quantum mechanics.